Visual Fraction Calculator

Welcome to the Fraction Calculator

This page hosts a fraction calculator that can perform addition, subtraction, multiplication or division of two fractions. The values for the calculation can be simple or mixed fractions, or consist of only wholes. Input of improper fractions is allowed. Enter the values directly into the corresponding locations in the fraction calculator and the answer will be updated in real time. A visualization of the operand fractions and the answer fraction is shown in the panel underneath where the values are entered.

Complete steps for solving each fraction operation are shown in the “See the Work” panel. Every calculation lists the worked solution — converting mixed numbers to improper fractions, taking the reciprocal for division, cross-cancelling, finding the common denominator, doing the arithmetic, reducing, and converting back to a mixed number — so the calculator illustrates not just the answers, but how each problem was solved. The answer also appears five ways: as a mixed number, an improper fraction, a decimal, a percent, and as a point on the number line.

If you wish to save the fraction calculator showing the problem you're working on, the “Share this Calculation” link can be copied and pasted into an email, your browser bookmarks or a web page. It will return to the fraction calculator and show the problem exactly as you see it.

Don’t just use this fraction calculator to race through your homework! Solve the problems on your own, and use the calculator to check your work or see how to work a problem you don’t understand. This fraction calculator is a useful tool, but it’s not a substitute for a powerful mathematical mind! There is no substitute for developing a solid set of concepts, so read on for a walkthrough of how fractions work, or pick a practice worksheet from the list above the instructions.

When we learn the basic math operations, we start by dealing with the operations on integers. But the world is full of partial amounts of things... A half cup of sugar in a recipe or six tenths of a mile or a quarter dollar. All of these represent a portion of a whole, and that’s exactly what a fraction is. We deal with partial amounts every day, so these ideas are familiar even if the way we have to work with them in math at first seems a little intimidating. Don’t worry! We’ll make it easy!

Real-World Uses for the Fraction Calculator

A fraction is a way to represent in mathematical terms a smaller part of a whole of something. So in our pizza example, if the whole pizza is cut into eight equal slices, and you eat three slices, you would have eaten three out of the eight parts of the whole. We represent this as a fraction as 3/8 and we say, “three eighths” when we read it aloud.

There are special terms for the numbers that make up a fraction. The number on the bottom is called the denominator. This is how many parts the whole is divided into. In our pizza example, the whole is divided into eight parts, so this fraction has a denominator of eight. The word denominator is a fancy word that simply means “the thing that divides.” Sometimes instead of denominator you may encounter the word divisor, but it’s the same thing.

Another way to think about a denominator is to understand it tells you how big each fractional piece is, so for example if our pizza is sliced into eight pieces, you can picture in your mind roughly how big each one is. If our pizza is sliced into 20 slices, you can imagine that each slice is going to be much smaller. This can be a stumbling block… As the denominator gets larger, each fractional part of the whole is actually smaller. This can be confusing when you are first learning about fractions because we are used to larger numbers corresponding to larger real-world values, but in this case a larger value in the divisor may actually make the value of the entire fraction smaller. For example, 1/8 is actually a bigger value (a bigger slice of pizza) than 1/20.

The top number in a fraction is called the numerator, which is just another fancy word that means “the thing that counts.” This represents the actual value in terms of how many parts of the whole are being represented by the fraction. In our pizza example, when you were really hungry and ate three slices, we represented that as the fraction 3/8. The numerator is three in this case and represents the three of the eight parts that make up the whole.

That’s really as complicated as it gets. A simple fraction just has two parts, the numerator on top and the denominator on the bottom. The denominator tells us how many pieces a whole is being divided into, and the numerator tells us how many of those pieces the fraction is meant to represent.

If this still seems a bit fuzzy, the fraction chart shows halves through sixteenths side by side so you can see how the size of each piece changes with the denominator.

Mixed Fractions and Improper Fractions with the Fraction Calculator

Mixed fractions represent some number of wholes, as well as a fractional part. Three and a half cups of sugar would be an example of something that you would represent with a mixed fraction.

Sometimes working with fractions in the steps you calculate a numerator larger than the denominator. This is called an “improper fraction.” An example would be something like 9/8, which means 9 parts of a whole, where each whole is divided into eight parts. If the divisor is telling us a whole is divided into eight parts, if we have nine parts we have enough for a complete whole with one part left over. So this means 9/8 is the same as one whole plus one part, or the mixed fraction 1 1/8.

When you are using the fraction calculator on this page, you can enter either improper fractions or mixed fractions and it will calculate the results for you appropriately, but the answer will always be given as a proper fraction.

Reducing Equivalent Fractions with the Fraction Calculator

If you’re really thinking about how fractions work, you might see that you can represent the same fractional amount with different fractions that have different denominators. If we go back to visualizing our pizza, if a whole is divided into four parts, half is going to be two slices. However, if the whole is divided instead into eight parts, half of the pizza would be four slices. In these examples, 2/4 and 4/8 are both the same amount of the whole. 2/4, 4/8 and 1/2 are all equivalent fractions because they represent the same real-world amount of a whole value.

Of course, the simplest way to represent any of those values is simply to say, “one half” and the fraction in simplest form that represents this is obviously 1/2. The two in this case is the smallest divisor possible that represents the fraction. Getting to the smallest possible divisor is called “reducing fractions” to their simplest form. This fraction calculator automatically reduces fractions in the answers.

Adding Fractions Calculator

To use this page as an adding fractions calculator, enter the two fractions and choose the plus operation — the sum appears instantly, reduced to simplest form. The process of adding fractions is straightforward if the denominators are the same. Simply add the numerators, and the resulting fraction has the same denominator. So one slice of pizza (1/8) plus another (1/8) equals two slices of pizza (2/8). That fraction could be reduced to 1/4, and mentally that makes sense because those two slices represent one quarter of the whole.

If you start with two fractions with different denominators, you need to find the least common denominator. This is the smallest denominator that will work to make equivalent fractions for each of the fractions you are attempting to add. For example, if we were trying to add 3/16 and 1/8, we could turn the 1/8 into the equivalent fraction 2/16. Now we are adding 3/16 and 2/16 which equals 5/16.

You can find more about common denominators in general at Wikipedia. If you need to find one by hand, the factoring calculator shows the factor pairs of any number, so run each denominator through it and the least common denominator is easy to spot.

Even though 2/16 is not a reduced fraction, for purposes of calculating the answer it’s okay to create non-reduced fractions or even improper fractions. We just want to return the fractions in proper reduced form when we provide an answer at the end.

Again, this fraction calculator does all of these steps for you, so if you need to see more examples, try a problem out and see how it works! Notice that when you are adding fractions, the visual preview in the fraction calculator shows how the two original fractions might combine to form the answer fraction.

Subtracting Fractions Calculator

When you use this tool as a subtracting fractions calculator, it finds the common denominator and handles any negative result for you. Subtracting fractions works much the same as adding fractions. You need to ensure the fractions have a common denominator, and then just subtract the numerators and reduce the answer fraction.

Just like with addition, if you are starting with a mixed fraction, you may need to convert the fraction to improper form to subtract the numerators. This is the reverse of the procedure we used to create proper fractions. To create an improper fraction, multiply the wholes by the denominator and add it to the numerator value. So 1 and 1/8 is the same as one whole plus one part, or eight parts plus one part, or a total of nine parts. So the proper mixed fraction 1 1/8 as an improper fraction is 9/8.

When subtracting fractions, if you take a larger fraction away from a smaller fraction, you will be left with a negative amount. You’ll show the resulting fraction with a negative sign on either the whole amount or the numerator. A negative fraction should only have one negative sign. A common mistake is to think you need to make both the numerator and the denominator negative if you have a negative answer. Don’t do this! If your answer is negative, you should only see one negative sign on the resulting fraction.

Multiplying Fractions Calculator

As a multiplying fractions calculator, this tool shows the product of two fractions in reduced form the moment you enter them. Multiplying fractions is in some ways less complicated than adding or subtracting fractions because you don’t need a common denominator. However, a good first step is to see if one or both of the fractions being multiplied can be reduced. This will make the calculations a little easier.

If either of the fractions are mixed, turn them into improper fractions as described above. If you are multiplying a fraction by a whole value, turn the whole into a fraction with a denominator of one, so for example the whole 3 is turned into the fraction 3/1 for the sake of doing the multiplication.

Next, to get the numerator for the answer, multiply the two numerators of the fractions you are starting with. To get the denominator, do the same thing, multiply the two denominators and write the result as the denominator in the answer fraction.

There’s a good likelihood that the resulting fraction is improper or could be reduced. You should always reduce your answer and put it in proper form. Again, if you need help with this, try a fraction multiplication problem using the fraction calculator on this page and it will show you an example. This fraction calculator will always simplify fractions in the answer.

Dividing Fractions Calculator

To work through a quotient with this dividing fractions calculator, choose the division operation and the reciprocal steps are applied for you. The procedure for dividing fractions is similar to multiplying fractions with one additional step. Start following the steps for multiplying fractions. As soon as you have the two fractions in improper form and you’re ready to multiply the numerators and denominators, you do one more step first. On the second fraction, swap the numerator and the denominator. So the old denominator goes on top and becomes the numerator, and the old numerator goes on bottom and becomes the denominator. Then, finish the procedure for multiplying fractions… Multiply straight across, reduce and simplify.

When you swap the numerator and denominator of a fraction, the result is something called a reciprocal. This procedure is sometimes called “inverting” or “taking the reciprocal” of a fraction. A reciprocal of a fraction has an interesting characteristic. If you multiply a fraction and a reciprocal of that fraction, the result will have the same number in the numerator and the denominator, which means it will reduce to one. Try it out in the fraction calculator by multiplying 2/3 by 3/2 and see.

Fraction Calculator with Whole Numbers

You can use this calculator with fractions and whole numbers together. To work with a whole number, enter it in the larger box to the left of a fraction and leave the numerator and denominator empty — or combine it with a fraction to make a mixed number. Internally, a whole number is treated like a fraction with a denominator of one, so adding, subtracting, multiplying or dividing whole numbers and fractions all work exactly the same way. Try 3 x 1/4 or 5 - 2/3 and watch how the whole number is handled in the answer.

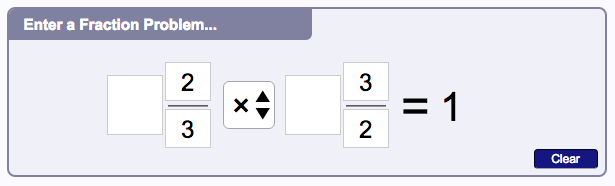
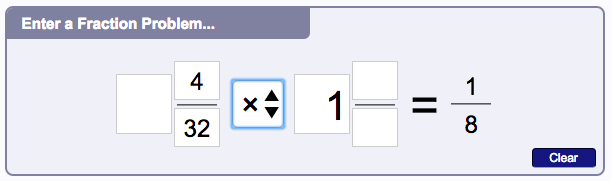
Simplify Fractions Calculator

This fraction calculator will automatically simplify results. If you need to simplify fractions, this fraction calculator can do the work for you by entering a regular fraction, mixed fraction or improper fraction and then multiplying the value by one. The fraction calculator will simplify the answer for you. For example, if you enter 4/32 x 1 in the fraction calculator, the simplified product is 1/8.

For a dedicated tool that shows the greatest common factor, the reduction step and a row of equivalent fractions, use the simplify fractions calculator.

Mixed Fraction Calculator

If you need a mixed number calculator, this tool handles mixed fractions for all operations and will return the result in simplest form. When the fraction calculator deals with mixed fractions, the procedure is almost always easier if the whole number is multiplied by the denominator and added to the numerator to create an improper fraction. This conversion from mixed numbers to improper fractions allows fraction problems to be treated just as though the whole numbers were not involved.

The fraction calculator does this internally to solve mixed fraction problems.

If mixed numbers are the whole job, the dedicated mixed number calculator opens on a mixed-number problem and walks through the conversion to improper fractions and back for every operation.

For adding fractions or subtracting fractions, the fraction calculator still needs to determine a common denominator. Then, after completing the operation, if the resulting fraction is still improper the fraction calculator converts it back to a mixed fraction for use as the answer.

Even once the fraction calculator factors a whole number out of an improper fraction, the resulting mixed fraction may not yet be in simplest form. If the fraction can be reduced, the fraction calculator will find a common divisor of both the numerator and the denominator and then divide both components to simplify the final fraction.

You're Ready for Fractions with Our Online Fraction Calculator

This page has given a very brief overview of fractions, and provided a number of examples that you can try in the fraction calculator. We covered adding fractions, subtracting fractions, multiplying fractions and dividing fractions, plus how to create a proper fraction from an improper fraction (and vice-versa), reducing fractions, finding a least common denominator, plus how to take a reciprocal of a fraction. You've seen how to use the fraction calculator to simplify improper fractions, and how to use the fraction calculator to reduce fractions. You can try all of these concepts in the fraction calculator, study the results and you’ll find you’re a fraction rock star in no time!

When you’re ready for more, try out the fractions worksheets below for practice and share this fraction calculator with your friends!

Put This Fraction Calculator on Your Website

Teachers, tutors and bloggers are welcome to embed the fraction calculator on their own pages. Copy the code below and paste it into your site’s HTML where you want the calculator to appear. The embedded calculator is free to use and links back to this page so your visitors can find the worked solutions and worksheets.

Further Reading on Fractions

• Introduction to fractions at Basic-Mathematics.com — another approach to the core concepts.
• Fraction concepts with illustrations at GCFGlobal.
• How to find common denominators at Quick and Dirty Tips.