Math Worksheets
Core Math Worksheets
Fraction Worksheets
Algebra
Other Worksheets
Place Value
Percentages
Rounding Numbers
Ordering Numbers
Standard, Expanded, Word Form
Mean Median Mode Range
Ratio Worksheets
Probability Worksheets
Roman Numerals
Factorization, GCD, LCM
Prime and Composite Numbers
Pre-Algebra
Geometry Worksheets
Blank Clocks
Telling Analog Time
Analog Elapsed Time
Greater Than and Less Than
Money
Arithmetic Sequences
Geometric Sequences
Venn Diagram
Graph Worksheets
Measurement & Conversions
Patterns and Puzzles
Color by Number
Holiday & Seasonal
Early Learning
Printables
Calculators
Math Worksheets by Grade
Worksheet News
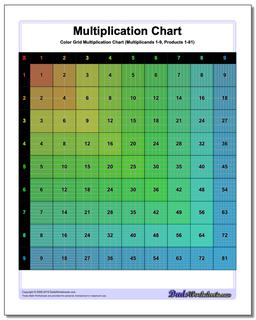
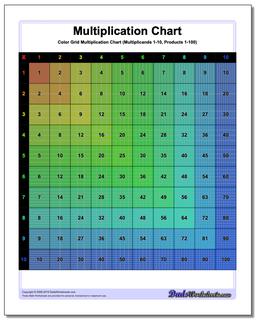
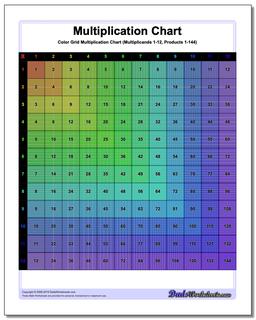
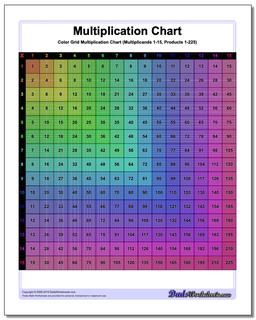
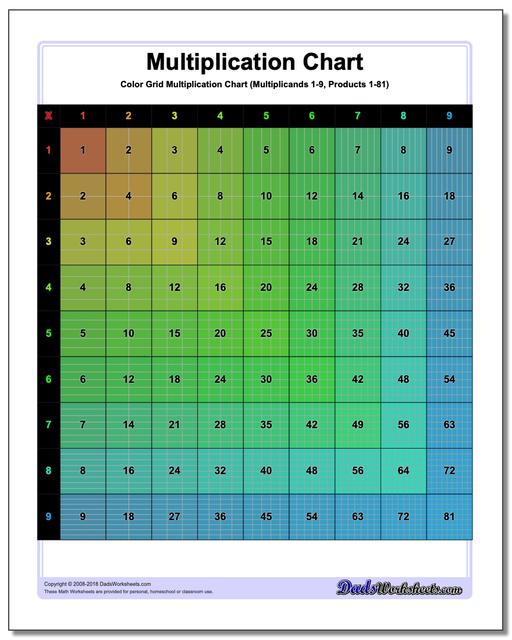
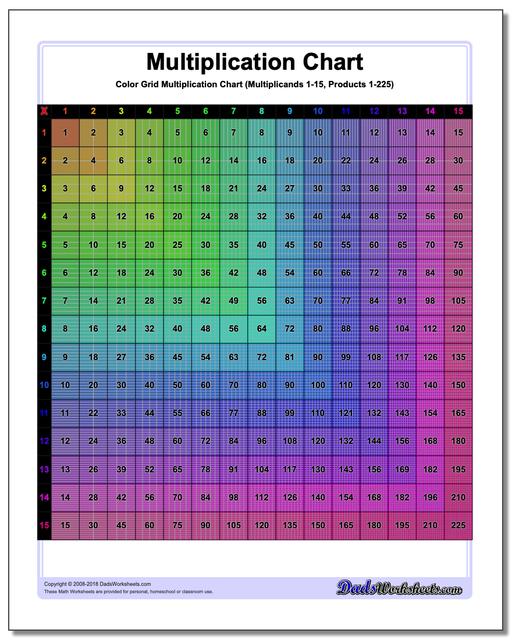
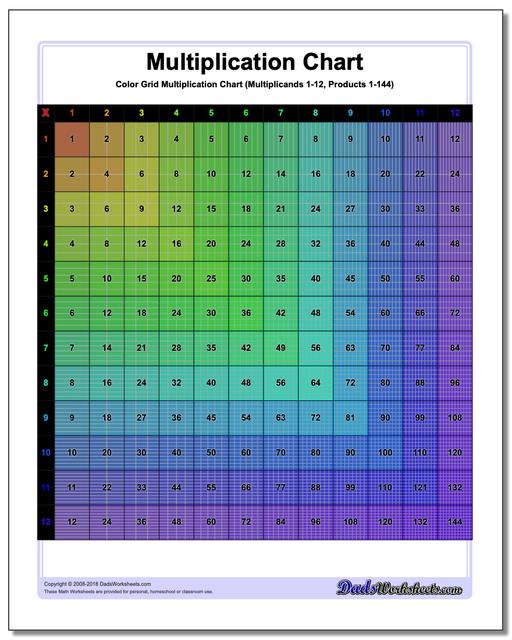
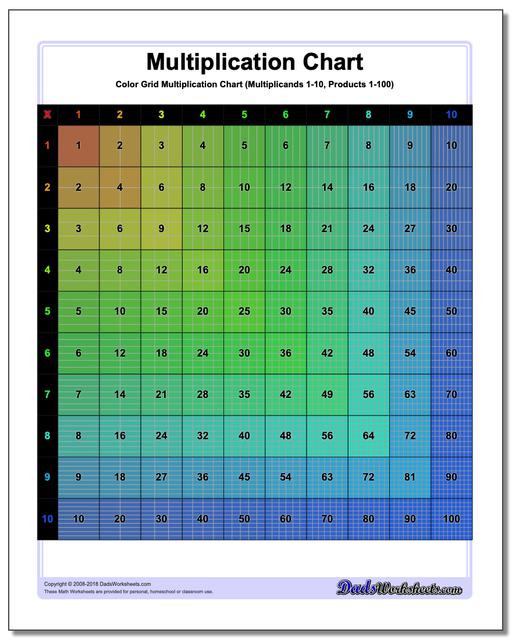
Multiplication Chart: Grid Multiplication Chart
This printable chart presents the multiplication table with cells divided to reflect the actual product. Separate black and white and color versions of the multiplication chart, each with ranges 1-9, 1-10, 1-12 and 1-15.
Colored Grid Multiplication Chart
Grid Multiplication Chart
Printable Grid Multiplication Chart
It can be helpful to visualize multiplication products when learning the times table, and these printable multiplication charts really help. Each version divides the products into cells, so the multiplication chart up 100 will have in its final cell 100 tiny squares. Don't try to count them.
Worksheet History




These are not the Multiplication Charts you are looking for?
Click to check out the main multiplication chart page... You'll find dozens of other options including cool color multiplication charts, multiplication charts with different ranges of products and much more...