Core Math Worksheets
Fraction Worksheets
Algebra
Other Worksheets
Place Value
Percentages
Rounding Numbers
Ordering Numbers
Standard, Expanded, Word Form
Mean Median Mode Range
Ratio Worksheets
Probability Worksheets
Roman Numerals
Factorization, GCD, LCM
Prime and Composite Numbers
Pre-Algebra
Geometry Worksheets
Blank Clocks
Telling Analog Time
Analog Elapsed Time
Greater Than and Less Than
Money
Arithmetic Sequences
Geometric Sequences
Venn Diagram
Graph Worksheets
Measurement & Conversions
Patterns and Puzzles
Color by Number
Holiday & Seasonal
Early Learning
Printables
Calculators
Math Worksheets by Grade
Worksheet News
Visual Long Division Calculator
Using the Long Division Calculator
Using this long division calculator is easy! Enter a divisor and a dividend in the boxes, and the calculator will show all the work necessary to solve the long division problem.
If you need a long division calculator that will not just supply the quotient, but show the work necessary to divide correctly, then you've found it. When you enter a quotient and a dividend, the problem itself becomes instantly part of the long division calculator's work showing the answer, and you can highlight portions of the division steps to see how they relate to each other.
How to Do Long Division
The long division steps are applied repeatedly to solve a long division problem.
Divide
See how many times the divisor goes into the smallest possible part of the dividend. This will give you a digit to use as part of the quotient.
Multiply
Take the quotient digit from the first step and multiply it by the divisor, writing it underneath the partial dividend to setup for a subtraction operation.
Subtract
Subtract the product from the prior step from partial dividend to get a remainder amount. This amount should always be less than the quotient.
Bring Down
Bring down digits from the dividend, extending the remainder from the prior step, until that amount is greater than the divisor, then repeat.
Repeat
Repeat until all of the digits have been brought down. Any result that cannot be further divided is the long division problem's remainder.
After you have brought down all of the digits, if the remaining number is less than the divisor, that value is the remainder. The long division calculator shows the remainder with an arrow carrying it back up to the quotient.
These are same steps the long division calculator uses to show the work for a long division problem when a remainder is generated. The first answer digit in the quotient is shown in the long division.
The hardest part of performing the long division steps by hand is the initial division step. Determining how many times the partial dividend is divided by the divisor can be tricky, especially when dealing with multiple-digit divisors. As a check, if the product of the multiplication step is larger than the divisor, you know that the partial quotient in the first step can be increased. You can observe this in the work shown in the long division calculator... Notice that the product of the multiply step is always less than the remainder.
An Example of Long Division with Remainders
The easiest way to understand long division is to see an example. This long division calculator lets you do that for any problem! You can enter a problem and explore the individual steps by hovering over portions of the work shown in the calculator, but even with that extra bit of help, long division can be difficult to understand. The example below walks through a problem using the same "show your work" output that the long division calculator generates for a typical problem. This should help you put the calculator's output in context and help you understand how to work long division problems on your own!
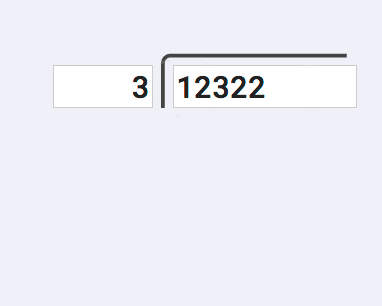
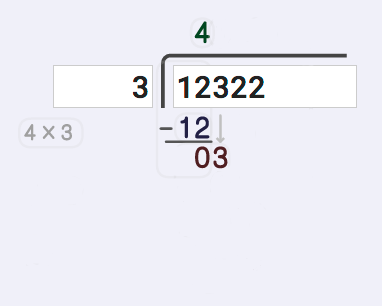
We'll work this example problem of 12322 divided by 3 that illustrates long division with remainders. This is a good problem because it shows some of the more complex steps for solving long division, and it's a dividend and divisor that produces a remainder.
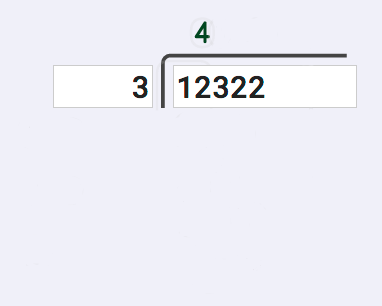
The first step in long division, the "divide" step, is to try to find the smallest part the dividend that can be divided by the divisor. Looking at the first digit in the dividend, we see that 1 cannot be divided by 3, so we need to continue and look at the second digit as well. 12 can be divided by 3, so we start out with a 4 as the first digit in the quotient.
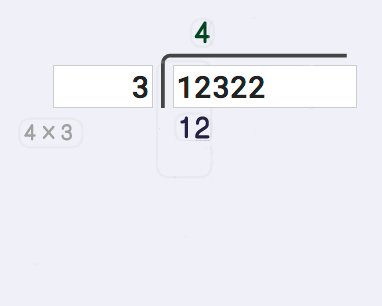
The next step, the "multiply" step, requires us to take that answer digit with just calculated, multiply it by the divisor. This gives us a product that we'll use in the next step. This is actually fairly easy because we just calculated 12 divided by 3 in the previous step, so we instantly know the product to write down. This gets trickier with multiple digit long division obviously, so don't underestimate this step...
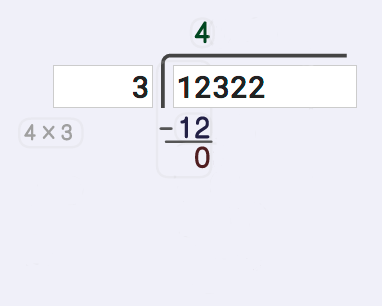
The next task following our long division steps is to subtract that product from the partial dividend. Because the partial quotient we've calculated so far may not be quite large enough, there may be some residual difference that we need to keep track of. In this case, 12 divided by 3 is exactly 4 without any remainder, so the result of this subtraction operation is zero. But hang on, because we'll see in a minute that this isn't always the case!
Now it's time to start bringing down digits from the dividend so that we have more to divide. This long division calculator shows this with a small grey arrow, and you can see these digits brought down add to the difference we calculated in the previous step. In this case, we bring down a 3, which divides very neatly into our divisor obviously, so we're done bringing down digits for this step.

Now it's time to divide again! And of course, 3 divided by 3 is one so we add that digit to our partial quotient, and we're ready to move on to our next step. And that means multiplication time again! That 3 divided by 3 math fact we just used shows up again here and the product of 3 times 1 gets written down to setup for the subtraction step.
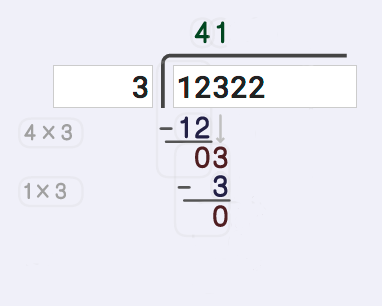
At this subtraction step, we trivially subtract 3 from 3 and get zero as our remainder this time. Don't be fooled, though! That doesn't mean we're finished! We still have digits remaining in the dividend that we haven't used, so let's keep going.

The next digit we haven't used from the quotient is is that 2, and the long division calculator brings that digit down next to the zero. We can't divide 3 by 2 and get a whole result, so we can't move on to the division step. But we did use a digit from the dividend, and we need to keep track of that. So we'll add that zero to the quotient for now, but what do we do next?

Bring down another digit! That gives us 22 divided by 3, which we definitely can do. Now 22 divided by 3 is a number greater than seven but less than 8, so we know they will be something left over, but that's okay. You'll
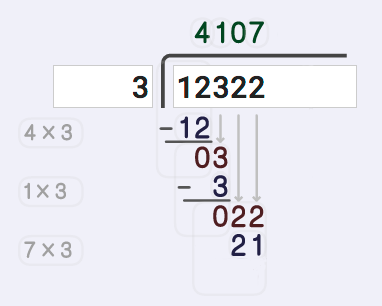
Time once more to multiply that digit from the quotient and setup for subtraction. Recall that 22 divided by 3 wasn't a perfectly even division, so we know we're going to get something slightly different for this multiplication step, and sure enough 3 times 7 is 21 and that's what we need to write.

Now it's time once more to subtract. 22 minus 21 gives us a difference of 1.

If our dividend were longer, we would start the process over again and start bring down digits, but we have exhausted the number of digits in the dividend, so we've come to the end of our long division steps. The difference we calculated in the last subtraction step becomes the remainder in the quotient and we're done!
More Resources for Learning Long Division
I hope this long division calculator is a big help figuring out the steps for long division and for seeing where remainders come from. But there are lots of great long division guides online.
Of coures, Wikipedia has a long discussion on long division which might be a little wordy, but about midway down there is a nice animated image that describes multiple digit divisors that inspired some of what this calculator shows in the work output.
If you're looking for a slightly different way to do long division, try watching this video on partial quotient division.
And, as always, Maria provides some great instructional video and detailed explanations over at the long division age at HomeSchoolMath.net.
Finally, one of the most important things you can do is practice! These long division worksheets are just some of the great resources at DadsWorksheets and they go great with this long division calculator for mastering this essential math skill!
Calculator Updates
| Date | Description |
|---|---|
| 02/20/2017 | This is the initial pass at a long division calculator with remainders. |
| 03/04/2017 | Enhanced highlighting of intermediate long division steps in the calculator's output where work is shown. |
