DadsWorksheets.com - Thousands of printable math worksheets for teachers, home schooling or general study!
Share to PinterestPinterestShare to FacebookFacebookShare to PocketPocketShare to TwitterTwitterShare to EmailEmailShare to FlipboardFlipboard
Math Worksheets

Core Math Worksheets

Fraction Worksheets

Word Problems

Algebra

Other Worksheets

Measurement & Conversions

Patterns and Puzzles

Color by Number

Holiday & Seasonal

Early Learning

Printables

Calculators

Math Worksheets by Grade

Worksheet News

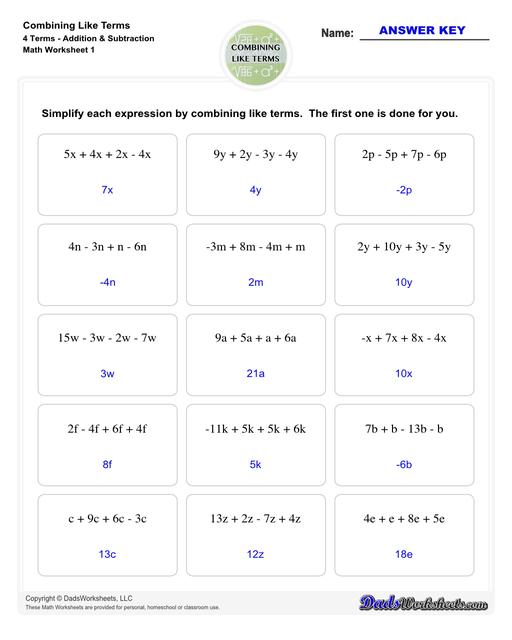
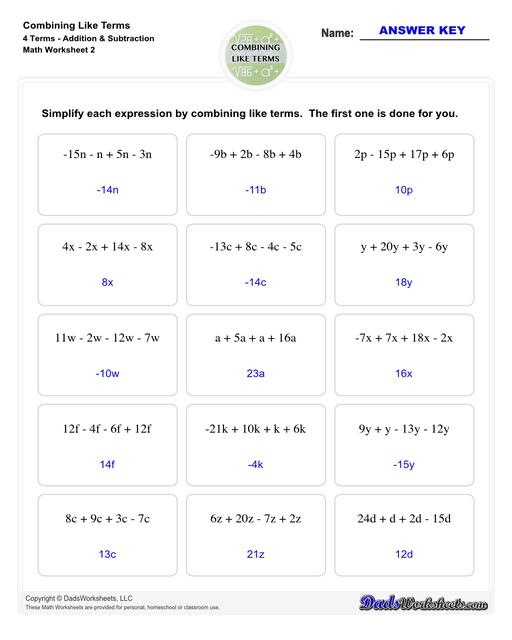
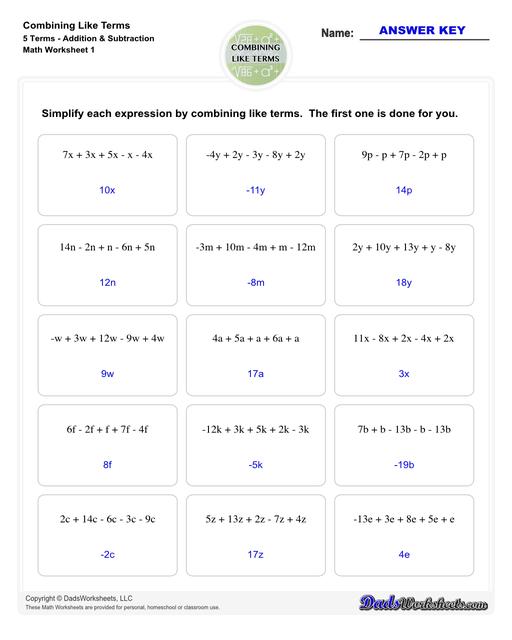
Combining Like Terms Worksheets

This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra.

Combining Like Terms (2 Terms)

This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 2 Terms Addition Subtraction V1 Combining Like Terms 2 Terms Addition Subtraction V1
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 2 Terms Addition Subtraction V2 Combining Like Terms 2 Terms Addition Subtraction V2
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 2 Terms Addition Subtraction V3 Combining Like Terms 2 Terms Addition Subtraction V3
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 2 Terms Addition Subtraction V4 Combining Like Terms 2 Terms Addition Subtraction V4

Combining Like Terms (3 Terms)

This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 3 Terms Addition Subtraction V1 Combining Like Terms 3 Terms Addition Subtraction V1
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 3 Terms Addition Subtraction V2 Combining Like Terms 3 Terms Addition Subtraction V2
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 3 Terms Addition Subtraction V3 Combining Like Terms 3 Terms Addition Subtraction V3
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 3 Terms Addition Subtraction V4 Combining Like Terms 3 Terms Addition Subtraction V4
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 3 Terms Addition Subtraction Multiplication V1 Combining Like Terms 3 Terms Addition Subtraction Multiplication V1
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 3 Terms Addition Subtraction Multiplication V2 Combining Like Terms 3 Terms Addition Subtraction Multiplication V2
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 3 Terms Addition Subtraction Multiplication V3 Combining Like Terms 3 Terms Addition Subtraction Multiplication V3
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 3 Terms Addition Subtraction Multiplication V4 Combining Like Terms 3 Terms Addition Subtraction Multiplication V4

Combining Like Terms (3 Terms)

This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 4 Terms Addition Subtraction V1 Combining Like Terms 4 Terms Addition Subtraction V1
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 4 Terms Addition Subtraction V2 Combining Like Terms 4 Terms Addition Subtraction V2
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 4 Terms Addition Subtraction V3 Combining Like Terms 4 Terms Addition Subtraction V3
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 4 Terms Addition Subtraction V4 Combining Like Terms 4 Terms Addition Subtraction V4
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 4 Terms Addition Subtraction Multiplication V1 Combining Like Terms 4 Terms Addition Subtraction Multiplication V1
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 4 Terms Addition Subtraction Multiplication V2 Combining Like Terms 4 Terms Addition Subtraction Multiplication V2
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 4 Terms Addition Subtraction Multiplication V3 Combining Like Terms 4 Terms Addition Subtraction Multiplication V3
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 4 Terms Addition Subtraction Multiplication V4 Combining Like Terms 4 Terms Addition Subtraction Multiplication V4

Combining Like Terms (5 Terms)

This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 5 Terms Addition Subtraction V1 Combining Like Terms 5 Terms Addition Subtraction V1
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 5 Terms Addition Subtraction V2 Combining Like Terms 5 Terms Addition Subtraction V2
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 5 Terms Addition Subtraction V3 Combining Like Terms 5 Terms Addition Subtraction V3
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 5 Terms Addition Subtraction V4 Combining Like Terms 5 Terms Addition Subtraction V4
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 5 Terms Addition Subtraction Multiplication V1 Combining Like Terms 5 Terms Addition Subtraction Multiplication V1
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 5 Terms Addition Subtraction Multiplication V2 Combining Like Terms 5 Terms Addition Subtraction Multiplication V2
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 5 Terms Addition Subtraction Multiplication V3 Combining Like Terms 5 Terms Addition Subtraction Multiplication V3
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 5 Terms Addition Subtraction Multiplication V4 Combining Like Terms 5 Terms Addition Subtraction Multiplication V4

Combining Like Terms (6 Terms)

This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 6 Terms Addition Subtraction Multiplication V1 Combining Like Terms 6 Terms Addition Subtraction Multiplication V1
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 6 Terms Addition Subtraction Multiplication V2 Combining Like Terms 6 Terms Addition Subtraction Multiplication V2
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 6 Terms Addition Subtraction Multiplication V3 Combining Like Terms 6 Terms Addition Subtraction Multiplication V3
This collection of algebra worksheets focuses on combining like terms. Expertly crafted, they provide ample practice to hone algebraic skills. Each PDF worksheet includes an answer key, facilitating easy self-assessment and effective learning. Perfect for students aiming to master the fundamental concept of combining like terms in algebra. Combining Like Terms 6 Terms Addition Subtraction Multiplication V4 Combining Like Terms 6 Terms Addition Subtraction Multiplication V4

Parts of an Algebraic Expression

Algebraic expressions are part of a math problem that has some unknown numbers hidden behind letters. This mathematical “phrase” is comprised of numbers, variables, and operations without an equal sign. Let us quickly know the parts of an algebraic expression before we learn how to combine like terms. Refer to the illustration below...

An illustration showing Parts of an Algebraic Expression

Variables: These are unknown numbers represented by letters, typically x, y, or z. The variables in the given expression above would be x and y.

Coefficients: These are the numbers that multiply the variables. See our example above. For 2x, the coefficient would be 2. Then for 3y, the coefficient would be 3.

Constants: These are the numbers we can see and can be easily recognizable numbers such as, 3, -5, or even 0, but could also be more complicated such as fractions like ¼, or square roots such as √8. The constant in our example above is -10.

Terms: A term could be a variable on its own, a constant on its own, or a combination of the two by multiplication or division. The terms above would be 2x, 3y, and -10.

Operator: A symbol that tells you what to do (add, subtract, etc.). The operators on our sample illustration are + and -.

Understanding Like Terms

Before we dive into the mechanics of combining like terms, let's clarify what "like terms" are in algebra. Like terms are terms that have the same variables and corresponding exponents. In simpler terms, they are terms that can be combined or added together because they represent the same kind of quantity.

For example, in the expression 4x+5x, these are like terms because they have the same variable: x. You could combine these terms and simplify the expression as 9x.

How about unlike terms? These are terms that have different variables, such as 2x and 3y. Because they are different, you can not simplify them any further. If your expression was 2x+3y+5y, that could be simplified as 2x+8y, but that’s as far as you can go.

How to Combine Like Terms?

Algebra is often seen as a formidable foe by students of mathematics, but it's a critical foundation for more advanced mathematical concepts. One of the fundamental skills in algebra is combining like terms, a process that simplifies complex expressions, making them more manageable and easier to work with. In this guide, we will explore the concept of combining like terms and why it's a crucial skill for any algebra student to master.

Addition and Subtraction of Like Terms

Here's a step-by-step process of combining like terms involving adding or subtracting terms with the same variables and exponents.

Step 1: Identify Like Terms. Begin by identifying the terms in the expression that have the same variables and exponents.

3x + 2y - 5x + 7y

Like terms are 3x and -5x, 2y and 7y.

Step 2: Add or Subtract: For like terms with addition or subtraction signs between them, simply add or subtract their coefficients. The variable part remains unchanged. Remember to take the sign in front.

In the expression 3x + 2y - 5x + 7y, we can combine like terms as follows:

3x - 5x becomes -2x
2y + 7y becomes 9y

Step 3: Reassemble: After combining like terms, reassemble the simplified expression.

In our example, the simplified expression is -2x + 9y.

AAddition, Subtraction, and Multiplication of Like Terms

Next, you will learn how to use the distributive property and combine like terms in order to solve more complex equations. This time, it involves adding, subtracting, and multiplying terms that have the same variables and exponents. Here are the steps:

Step 1: If you see a parenthesis, with more than one term inside, then distribute first. Take note of how I distribute first before applying the rules for solving equations.

2 (3x + 2y - 5x + 7y)

style="padding-top:8px;"Step 2: Rewrite your equations with like terms together. Take the sign in front of each term. Multiply 2 one by one with all the terms inside the parenthesis.

2 (3x + 2y - 5x + 7y)
6x + 4y - 10x + 14y

Step 3: Combine like terms.

2 (3x + 2y - 5x + 7y)
6x + 4y - 10x + 14y
6x - 10x becomes -4x
4y + 14y becomes 18y

In our example, the simplified expression is -4x + 18y.

Tips on Combining Like Terms

Here are some tips and tricks to help you effectively combine like terms:

  • Identify like terms: Like terms are terms that have the same variables raised to the same exponents. For example, in the expression, 3x + 2y - 5x - 7y, 3x and -5x are like terms because they both have 'x' as the variable with the same exponent, and 2y and -7y are like terms for the same reason.
  • Group like terms: To combine like terms, group them together. This makes it easier to see which terms can be added or subtracted from each other.
  • Add or subtract coefficients: Once you've grouped like terms together, simply add or subtract the coefficients (the numbers in front of the variables) to combine them. Be sure to pay attention to the signs (+ or -) when combining terms.
    • Example 1: 3x - 5x becomes -2x
    Example 2: 2y - 7y becomes -5y
  • Keep constants separate: Constants (terms without variables) are also like terms. Combine them separately. For example, in the expression 6x + 3 - 2x - 5, first combine the x-terms (6x and -2x) and then combine the constants (3 and -5).
    • Combined x-terms: 6x - 2x becomes 4x
    Combined constants: 3 - 5 becomes -2
  • Watch for zero coefficients: If adding or subtracting like terms results in a coefficient of zero, you can omit that term from the expression since it doesn't affect the overall value.
  • When adding and subtracting numbers it's important to be consistent with positive and negative values. Depending on the magnitude and sign of the values, as well as the operation, your result may be positive or negative. This is a great opportunity to use a number line to locate the first operand and then careful consider the direct the operation and the sign of the second operand will move you to get the final result.
  • When numbers are multiplied or divided, two positive numbers will result in a positive sign. When two negative numbers are multiplied or divided, the result will have a positive sign. When there’s one number with a negative sign and the other with a positive sign, the result will have a negative sign.
  • Use parentheses when necessary: Sometimes, you may need to use parentheses to clarify which terms should be combined first. For example, in the expression 3(2x + 4) - 2(3x - 1), distribute the constants inside the parentheses before combining like terms.
    • 3(2x + 4) - 2(3x - 1)
    6x + 12 - 6x + 2
    14
  • Practice: Combining like terms becomes easier with practice. Work on various algebraic expressions to improve your skills.

The Purpose of Combining Like Terms

Why do we bother with combining like terms? The primary purpose is to simplify algebraic expressions. By combining like terms, we can reduce the complexity of an expression and make it more concise. This simplification makes the expression easier to understand and paves the way for solving equations and inequalities more efficiently.

Like any skill, mastering the art of combining like terms requires practice. Worksheets, exercises, and real-world problems are excellent ways to hone this skill. Whether you're a student tackling algebra for the first time or someone returning to algebraic concepts, remember that combining like terms is a crucial step on your mathematical journey. It's a skill that not only opens doors to more advanced math but also enhances problem-solving abilities in everyday life. It is a fundamental skill that simplifies expressions, aids in solving equations, and has real-world applications. By understanding the concept and practicing regularly, students and learners of all levels can confidently navigate the world of algebra and mathematics. So, embrace the challenge, practice diligently, and master the art of combining like terms to unlock the full potential of algebraic problem-solving.

Combining Like Terms Worksheets
WorksheetsCalculatorsAboutContactPrivacy