Core Math Worksheets
Fraction Worksheets
Algebra
Other Worksheets
Place Value
Percentages
Rounding Numbers
Ordering Numbers
Standard, Expanded, Word Form
Mean Median Mode Range
Ratio Worksheets
Probability Worksheets
Roman Numerals
Factorization, GCD, LCM
Prime and Composite Numbers
Pre-Algebra
Geometry Worksheets
Blank Clocks
Telling Analog Time
Analog Elapsed Time
Greater Than and Less Than
Money
Arithmetic Sequences
Geometric Sequences
Venn Diagram
Graph Worksheets
Measurement & Conversions
Patterns and Puzzles
Color by Number
Holiday & Seasonal
Early Learning
Printables
Calculators
Math Worksheets by Grade
Worksheet News
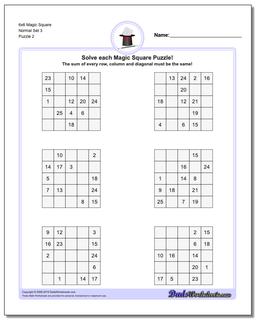
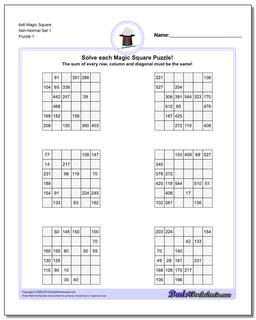
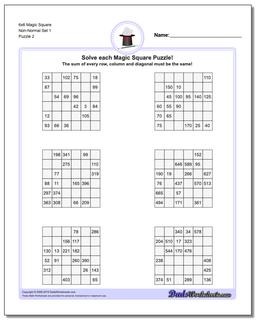
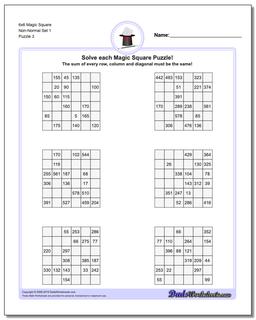
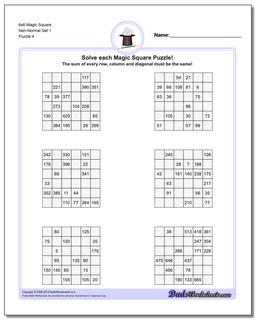
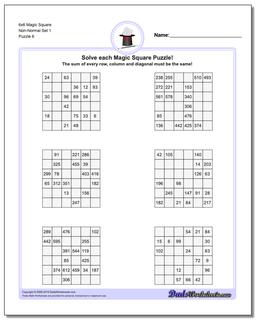
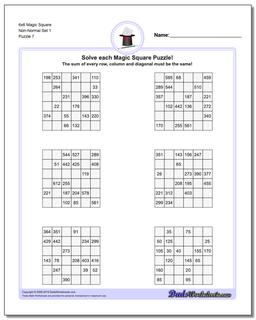
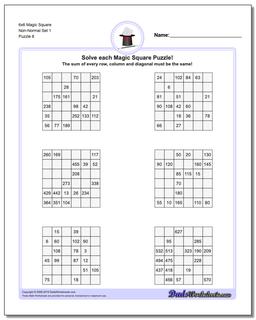
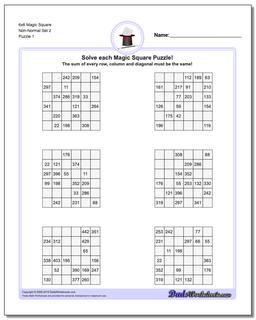
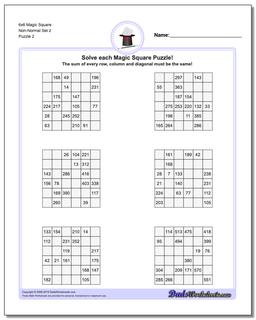
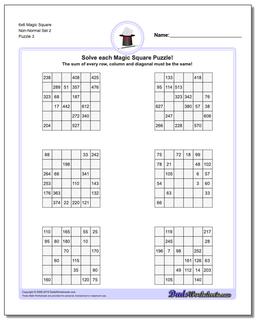
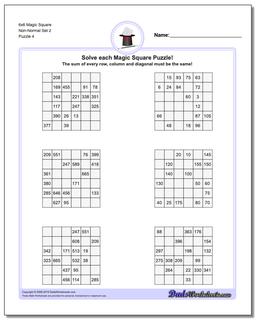
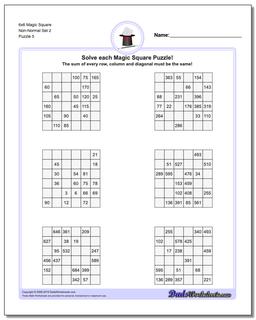
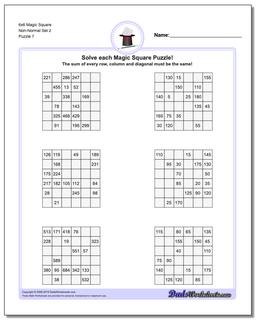
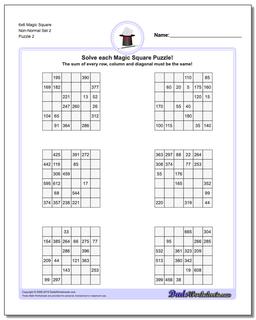
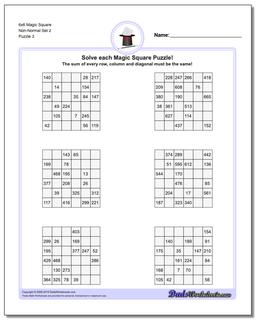
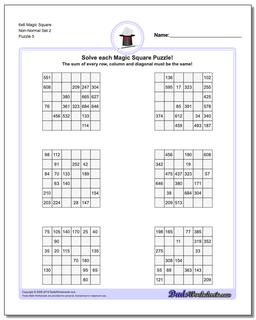
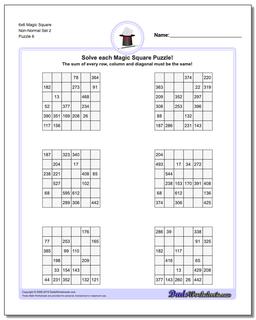
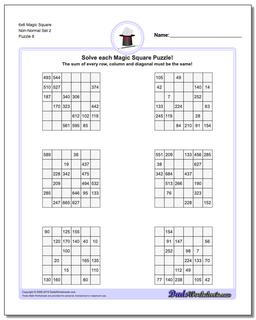
6x6 Magic Square
Thse worksheets start with normal 6x6 magic squares having numbers from 1-36, but the non-normal versions of the 6x6 puzzles are tremdously difficult to solve and will likely require your calculator and some time.
These 6x6 Magic Square Puzzle Worksheets are Very Difficult
These 6x6 magic squares, even in their normal forms, are quite challenging and good brian teasers for middle school math wizards or even for math savvy adults.
The worksheets with normal variations of these puzzles (6x6 puzzles that contain 1-36 in their cells) have a magic constant of 111 no matter how the numbers are arranged in each puzzle. Just because you know the magic constant, don't think these are easy though!
The later puzzles in this section are non-normal magic squares, so the sums for those puzzles will be a value larger than 111..
I am unaware of an method to derive the exact number of magic squares in an order 6 grid, but research using statistical techniques suggests it's a value near 17,700,000,000,000,000,000. By sheer coincidence I'm sure this is roughly (ignoring for currency conversion) the construction cost of the Death Star.
I'm serious, you can't make this stuff up.
But if you are aware of an algorithm for computing the maximum number normal magic squares of order-n (short of exhaustive search obviously), let me know as I'm somewhat curious...