Core Math Worksheets
Fraction Worksheets
Algebra
Other Worksheets
Place Value
Percentages
Rounding Numbers
Ordering Numbers
Standard, Expanded, Word Form
Mean Median Mode Range
Ratio Worksheets
Probability Worksheets
Roman Numerals
Factorization, GCD, LCM
Prime and Composite Numbers
Pre-Algebra
Geometry Worksheets
Blank Clocks
Telling Analog Time
Analog Elapsed Time
Greater Than and Less Than
Money
Arithmetic Sequences
Geometric Sequences
Venn Diagram
Graph Worksheets
Measurement & Conversions
Patterns and Puzzles
Color by Number
Holiday & Seasonal
Early Learning
Printables
Calculators
Math Worksheets by Grade
Worksheet News
Angles of Triangles Worksheets
The worksheets on this page require grade school students to solve problems related to the angles of triangles, including calculating interior angles, calculating exterior angles and calculating the lengths of line segments created from triangle angle bisectors. Click the images below to open each PDF worksheet with answer keys and get your triangle geometry practice started!
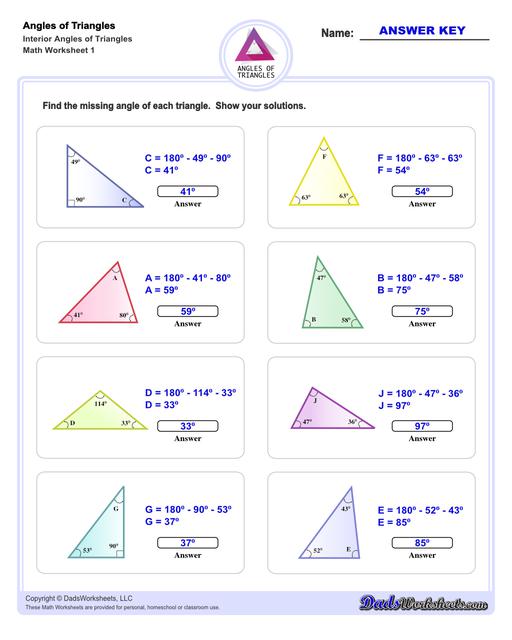
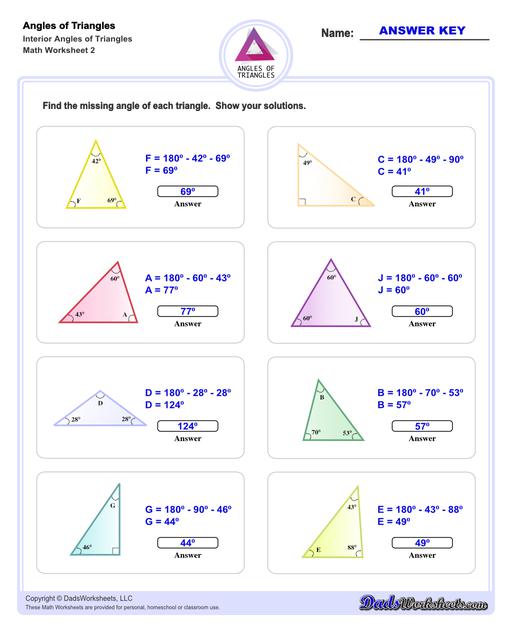
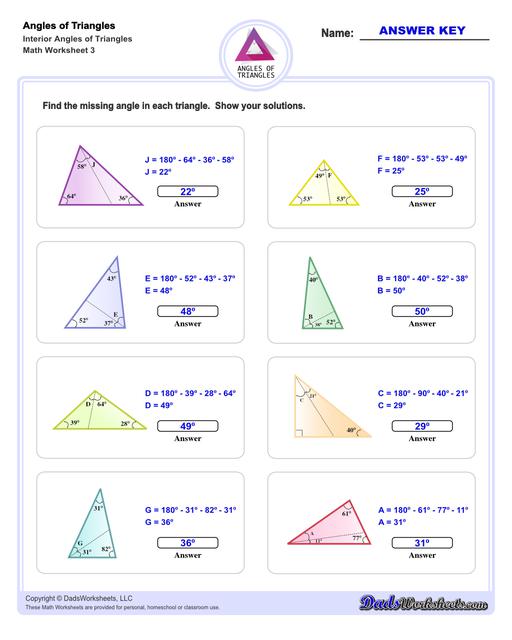
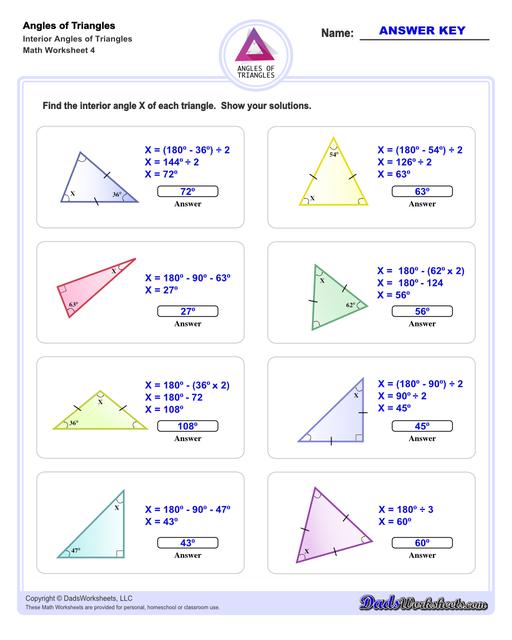
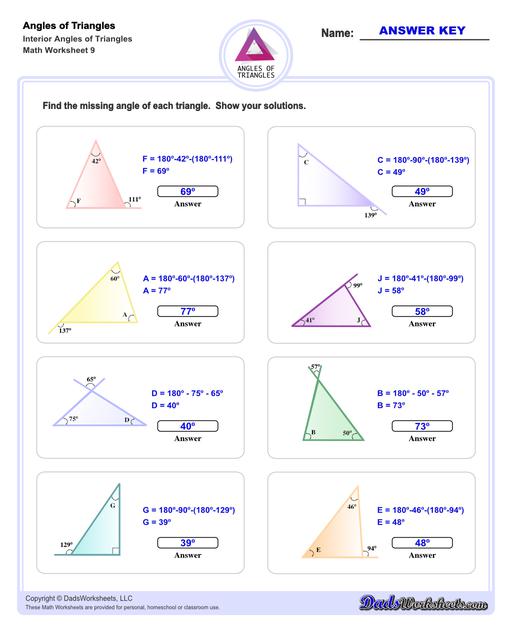
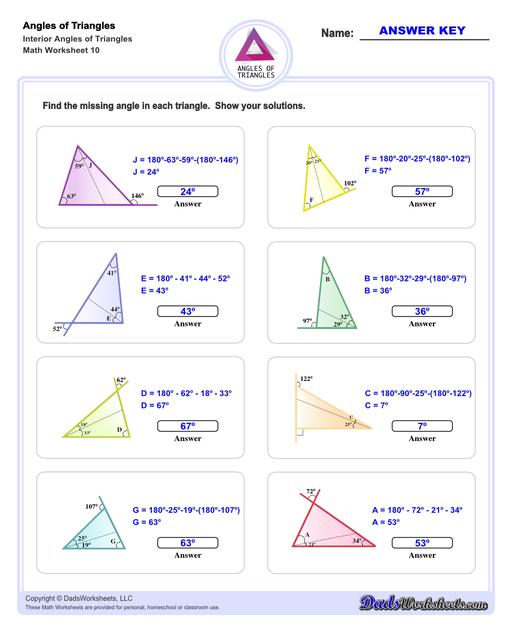
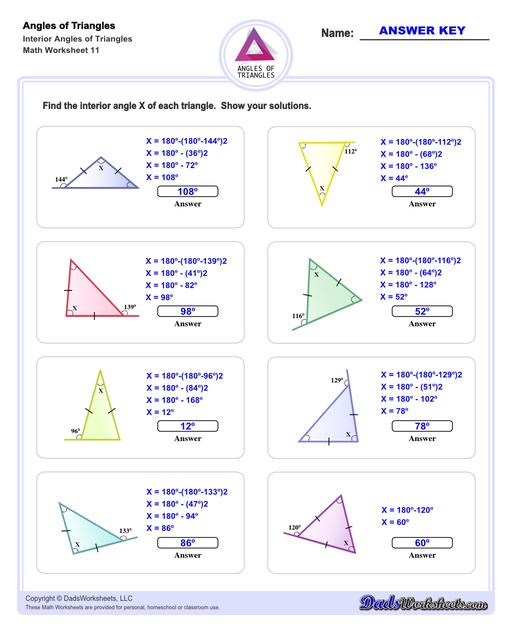
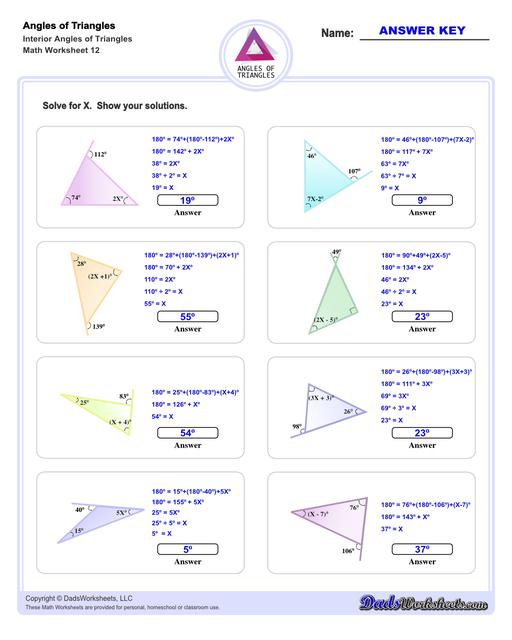
Interior Angles of Triangles Worksheets
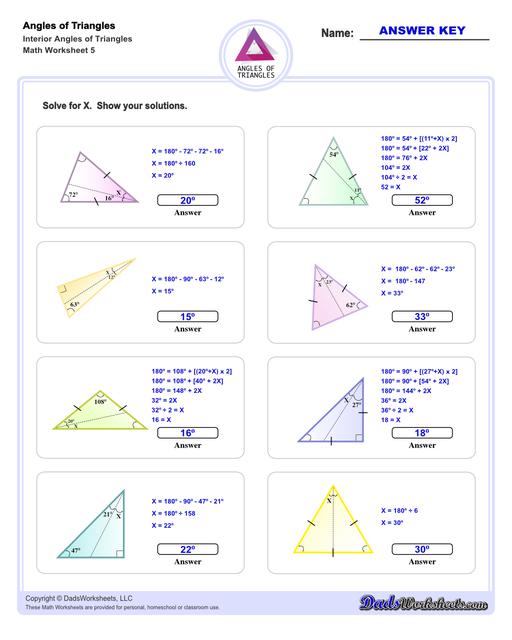
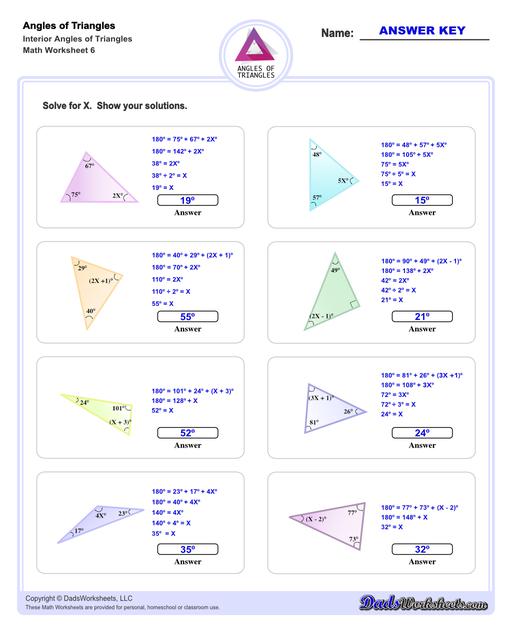
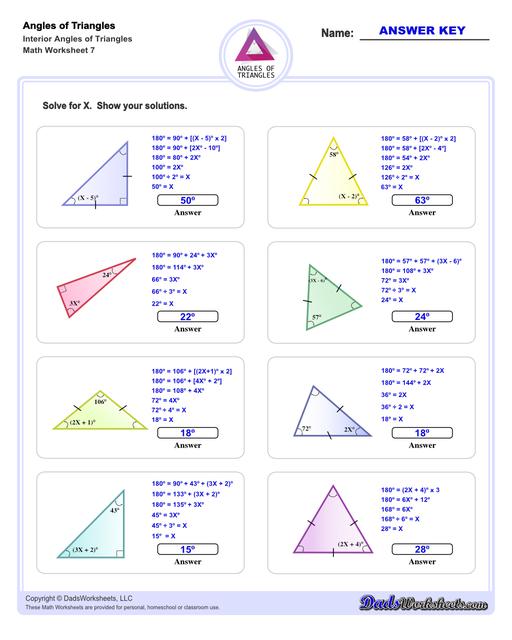
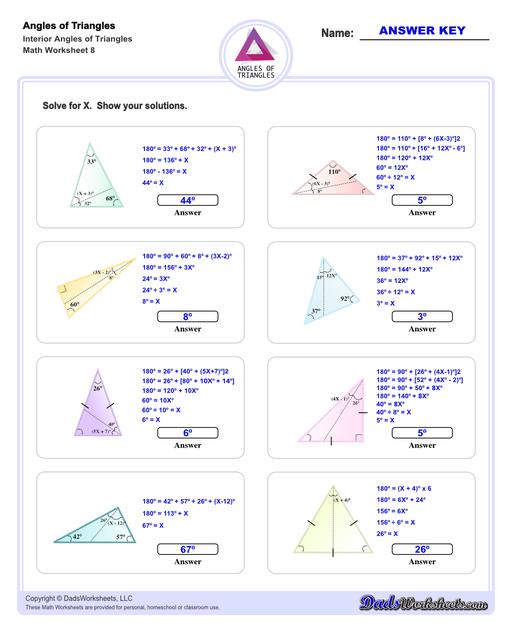
These triangle worksheets make use of the Triangle Sum Theorem which states that the sum of the interior angles of a triangle is always 180 degrees. More details on how to use this triangle postulate to calculate missing angles are discussed at the bottom of this page.
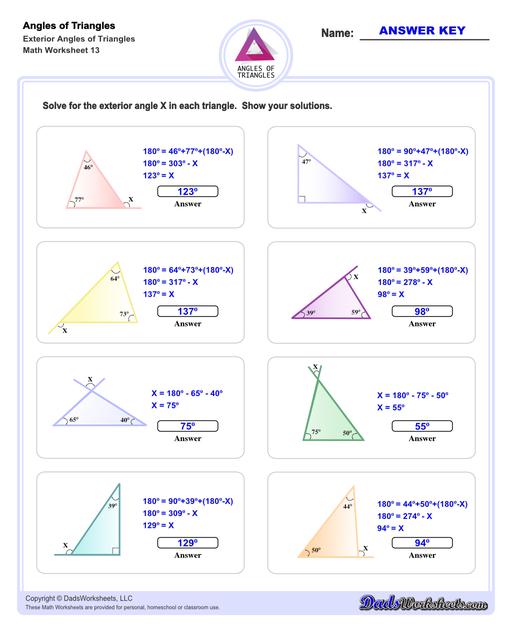
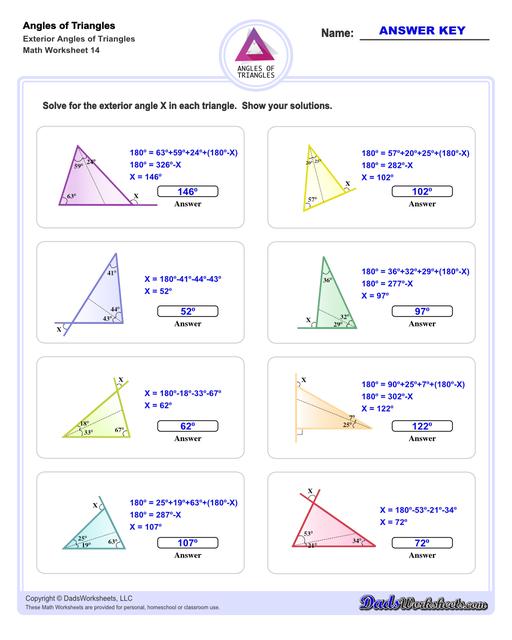
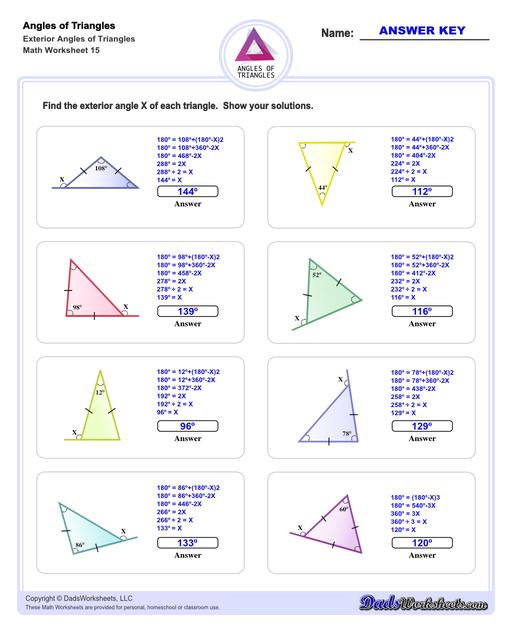
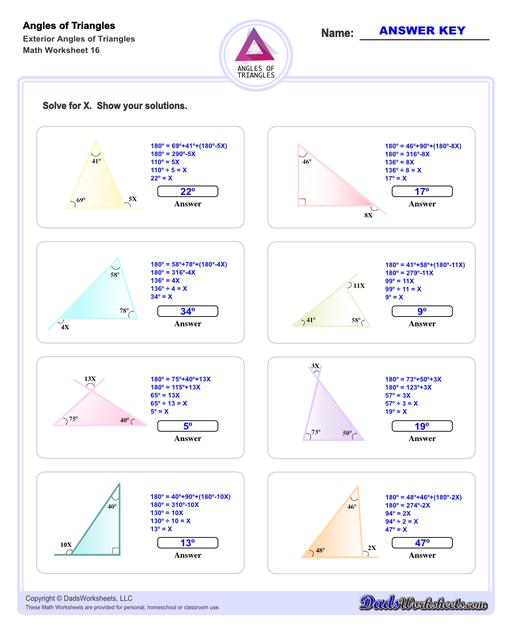
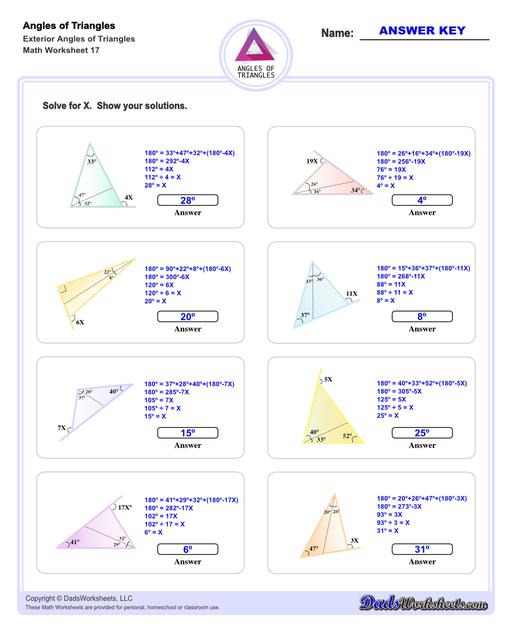
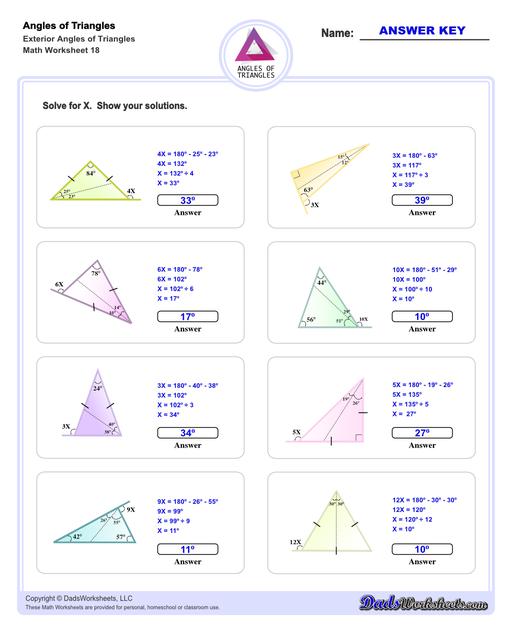
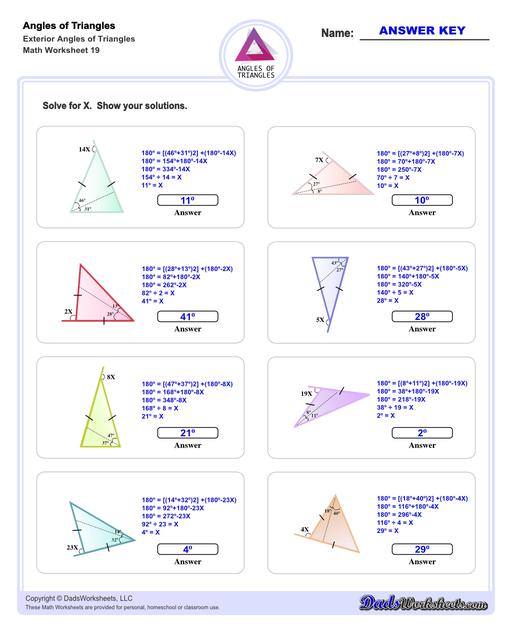
Exterior Angles of Triangles Worksheets
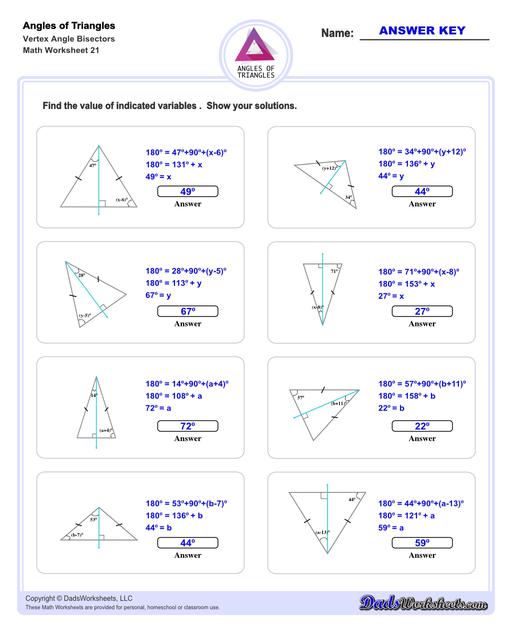
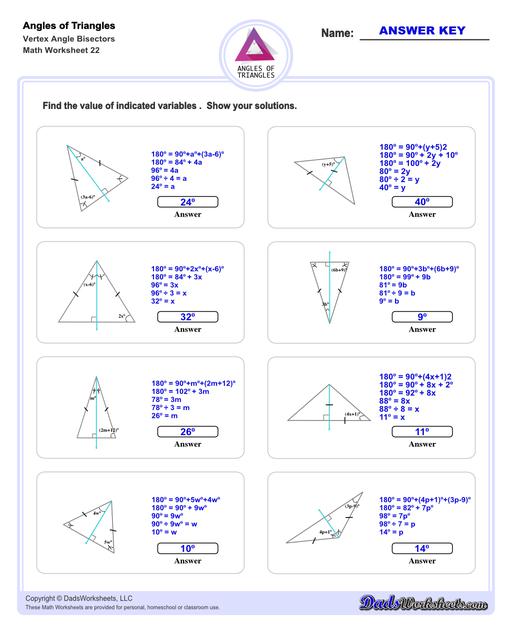
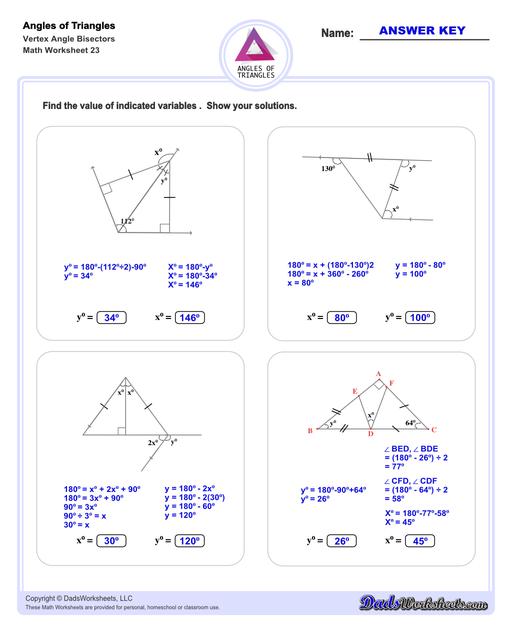
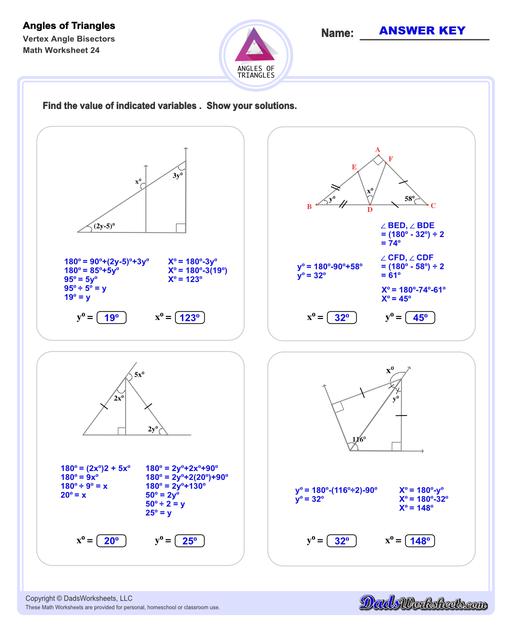
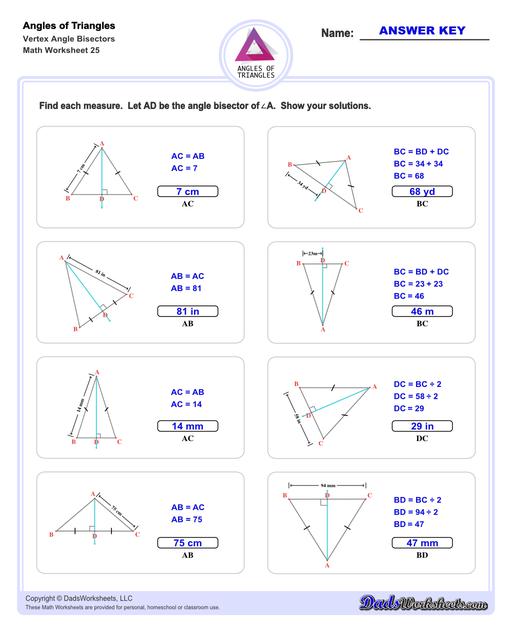
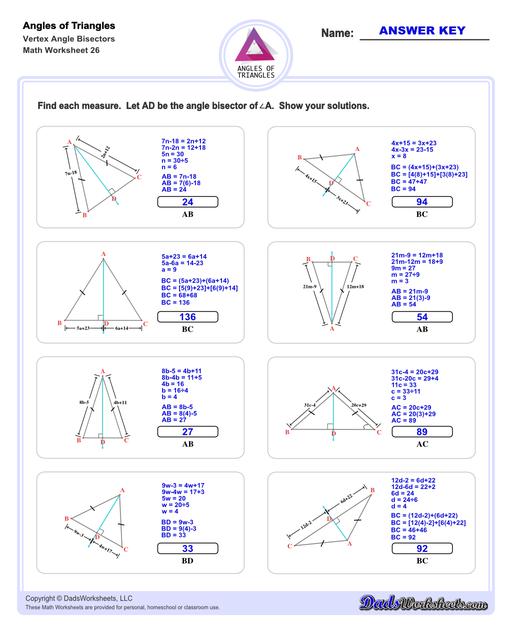
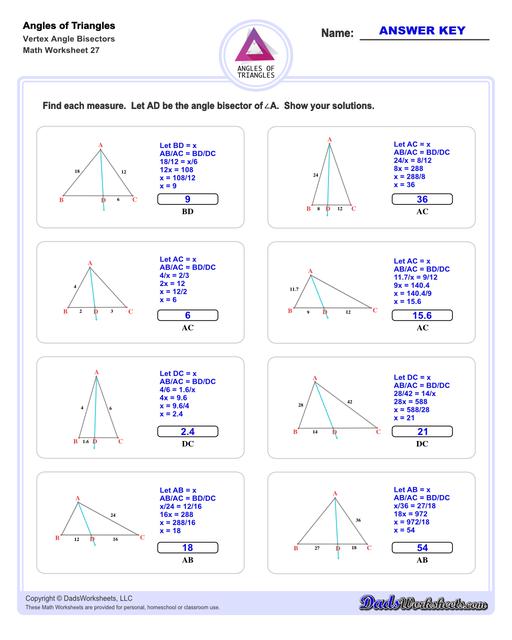
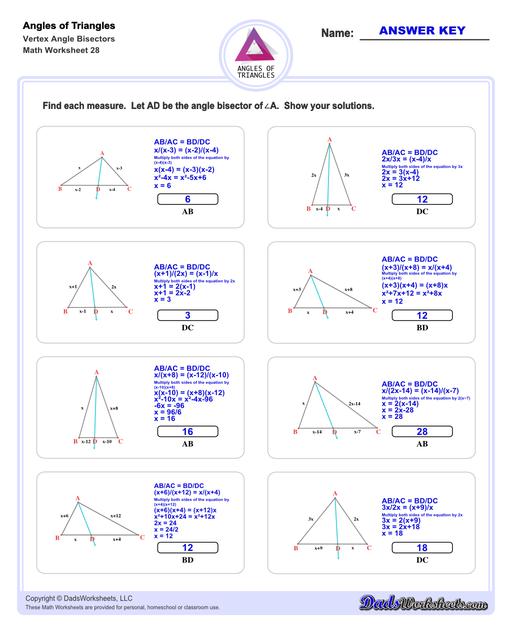
Triangle Vertex Angle Bisector Worksheets
Calculating Interior Angles of Triangles
The sum of the angles of a triangle postulate can be used to find a missing interior angle of a triangle given the other two angles.
Triangle Sum Theorem
If you know two of the three angles of a triangle, you can use this postulate to calculate the missing angle's measurement. For example, if ∠A and ∠B are known, ∠C can be calculated using the following equation...
Formula for Calculating a Missing Interior Angle of a Triangle
A common problem is calculating a missing angle in a right triangle. In these triangle problems, we know that one of the angles must be exactly 90° therefore only one other angle must be known to calculate the third missing angle:
Formula for Calculating a Missing Interior Angle of a Right Triangle
Another common problem involves finding the two base angles for an isosceles triangle given the triangles vertex or apex angle. Because the legs of an isosceles triangle are equal, the corresponding adjacent angles at the triangles base are also equal, so calculating the measure of the leg angles involves substracting the vertex angle from 180° and dividing the result among the two remaining angles:
Formula for Calculating Base Angles of an Isosceles Triangle
Calculating Exterior Angles of Triangles
The exterior angle of a triangle is calculated using the properties of supplementary angles. By extending a line from one of the triangle's sides, the exterior angle can be calculated from the adjacent interior angle by subtracting that angle from 180°. Conversely, the interior angle can be calculated by from the exterior angle using procedure. The triangle worksheets on this page provide practice calculating interior angles given exterior angles, or calculating exterior angles given interior angles.
Triangle Angle Bisector Theorem
An angle bisector of a triangle is a line that divdes one of the triangle's interior angles in half. The resulting line segment splits to opposite side of the triangle into two line segments. The Triangle Angle Bisector theorem states that the angle bisector divides the opposite side into two line segments that are proportionate to their adjacent sides. The triangle angle bisector worksheets on this page allow students to practice determining the length of these bisected sides for different types of triangles, starting with equilateral and isosceles triangles (where the bisected segments are equal), and progressing more generally to obtuse and acute triangles where the proportionate relationship is used to calculate two different lengths.