Center of Triangle

Center of triangle worksheets for practice finding the centroid of a triangle, orthocenter of a triangle, and circumcenter of a triangle. Checkout the worksheets below, or scroll down for detailed steps on the calculating the various types of triangle centers...

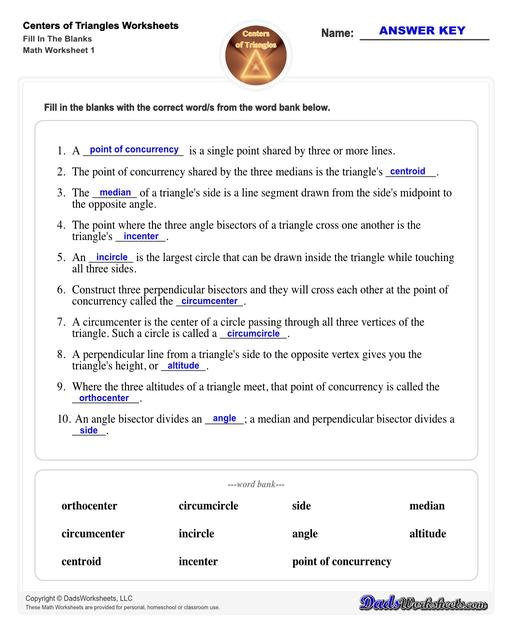
Center of Triangle Vocabulary

---

Fill In The Blanks V1

Fill In The Blanks V2

Fill In The Blanks V3

Fill In The Blanks V4

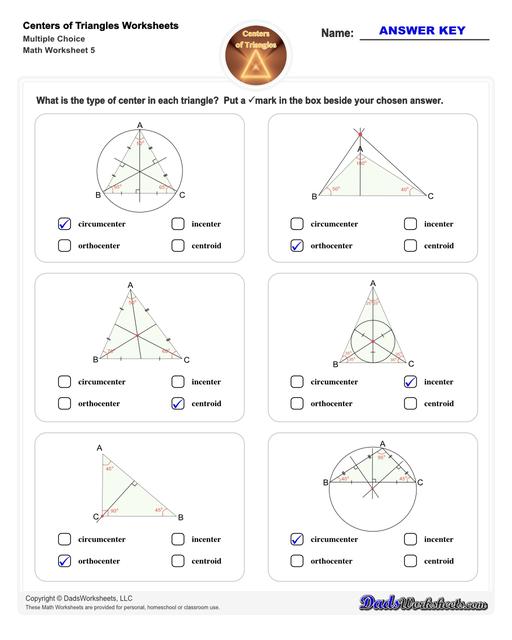
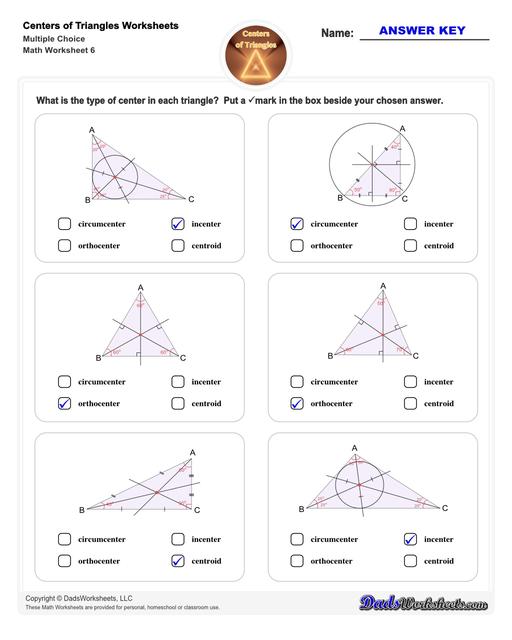
Center of Triangle Multiple Choice

---

Multiple Choice V1

Multiple Choice V2

Multiple Choice V3

Multiple Choice V4

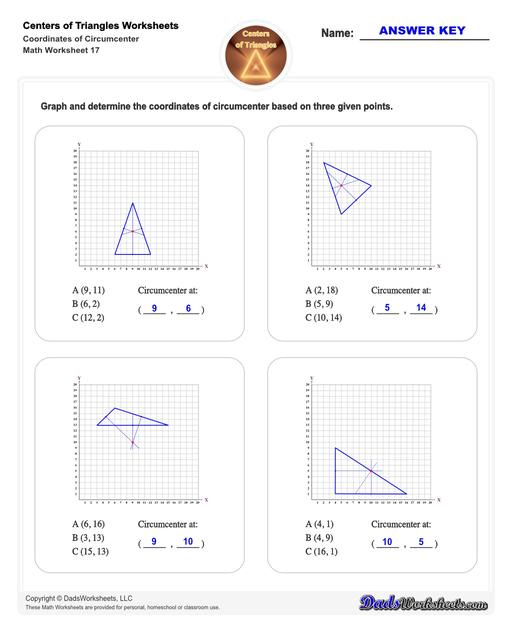
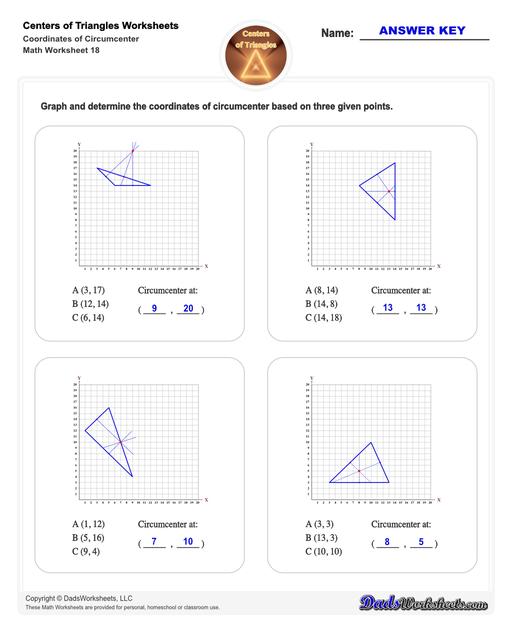
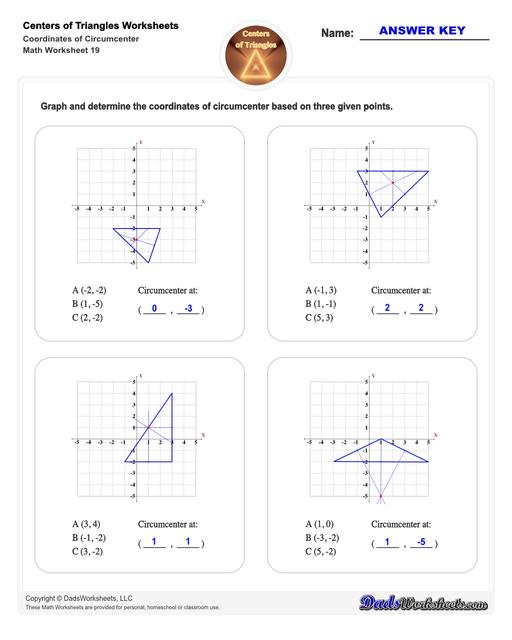
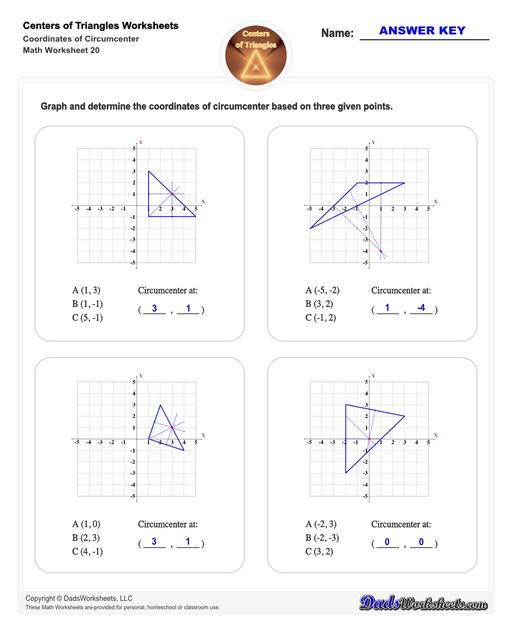
Center of Triangle Calculate Circumcenter

---

Coordinates Of Circumcenter V1

Coordinates Of Circumcenter V2

Coordinates Of Circumcenter V3

Coordinates Of Circumcenter V4

Center of Triangle Calculate Incenter

---

Coordinates Of Incenter V1

Coordinates Of Incenter V2

Coordinates Of Incenter V3

Coordinates Of Incenter V4

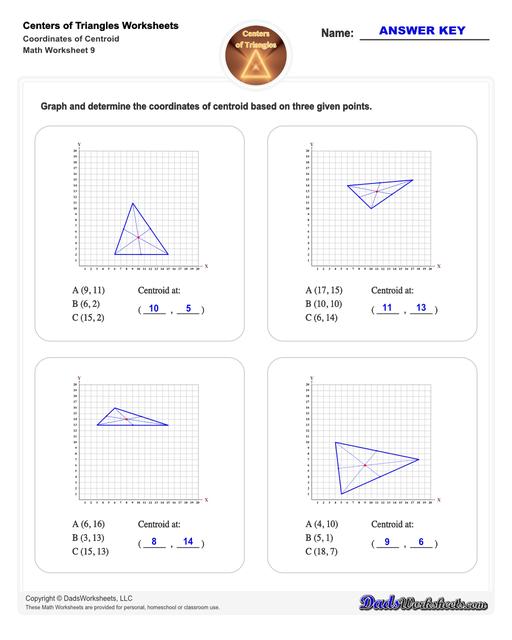
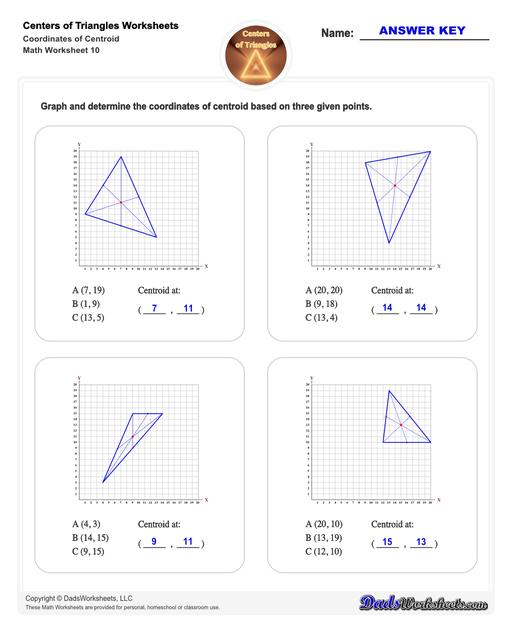
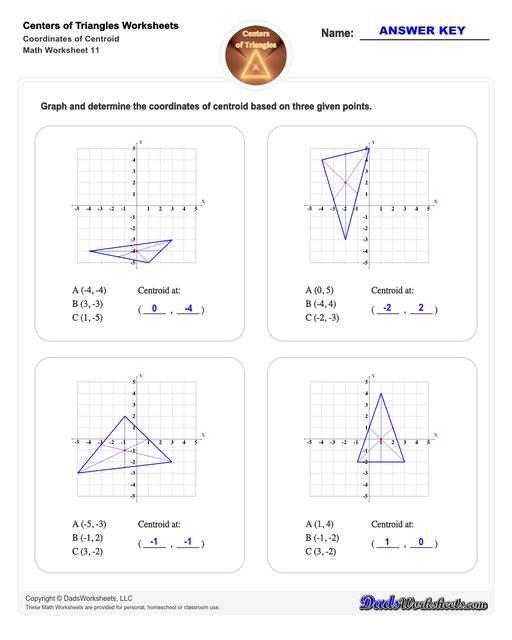
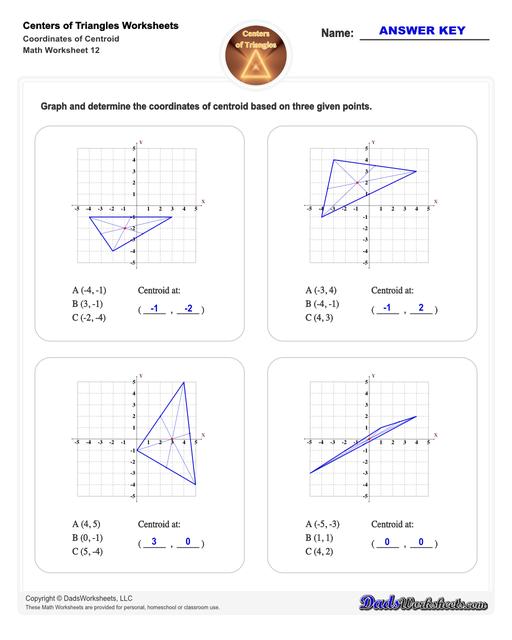
Center of Triangle Calculate Centroid

---

Coordinates Of Centroid V1

Coordinates Of Centroid V2

Coordinates Of Centroid V3

Coordinates Of Centroid V4

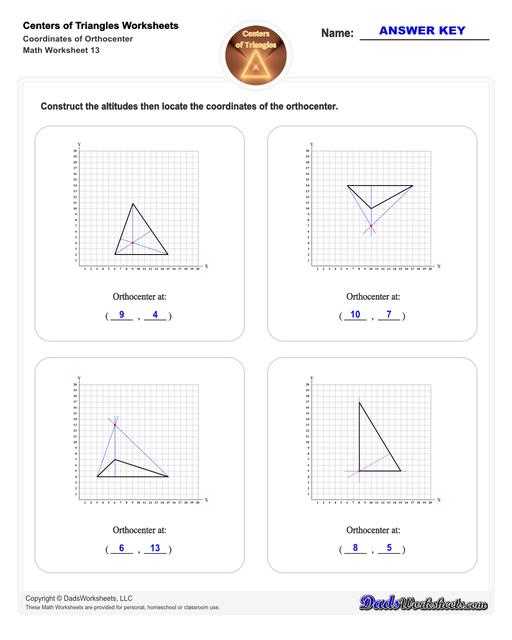
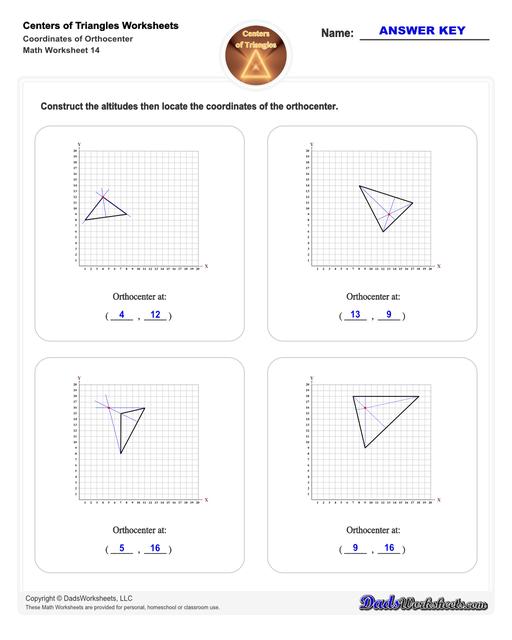
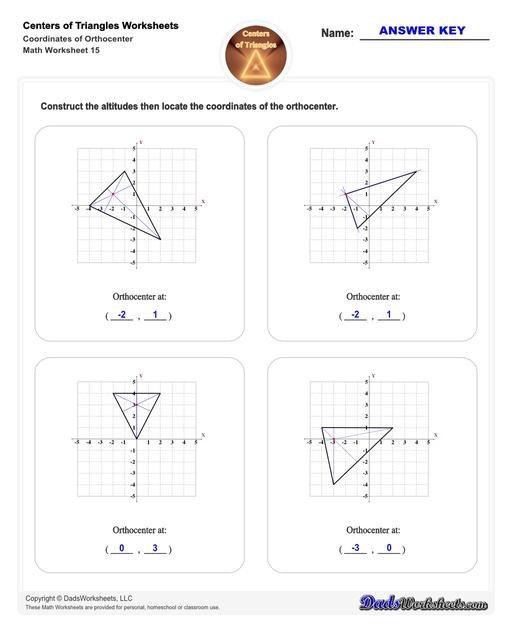
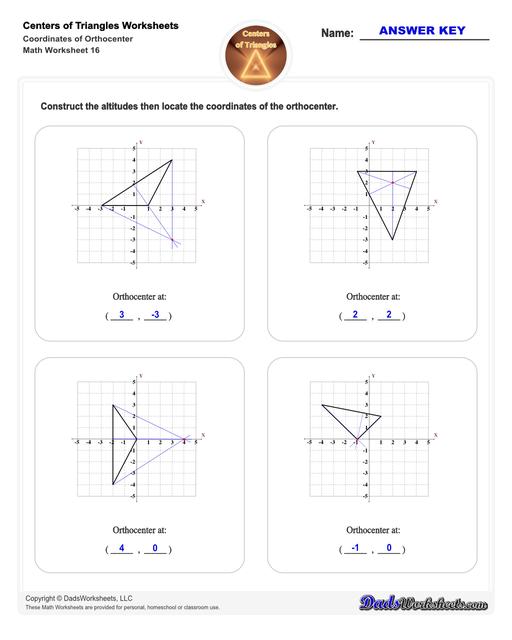
Center of Triangle Calculate Orthocenter

---

Coordinates Of Orthocenter V1

Coordinates Of Orthocenter V2

Coordinates Of Orthocenter V3

Coordinates Of Orthocenter V4

Calculating the Centers of Triangles

The Centers of Triangles worksheets on this page start with requiring students to check what they have learned about the basic concepts of triangle centers by filling in the blanks on each sentence. A word bank is provided at the bottom of the worksheets. Here’s a tip for you when a word bank is provided: Always do the easiest and most obvious questions first then use the process of elimination.

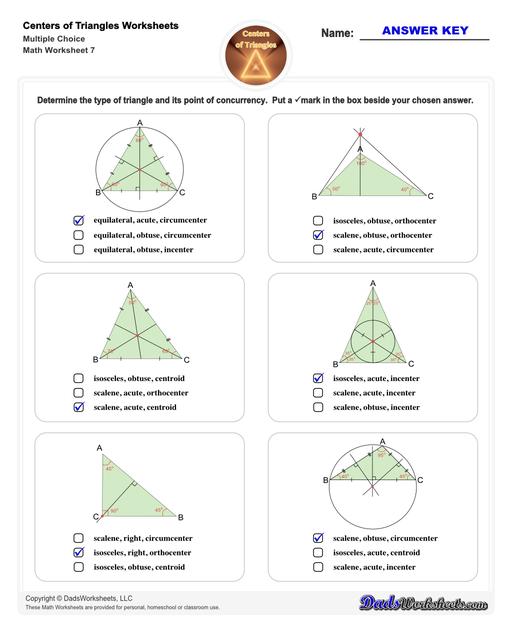
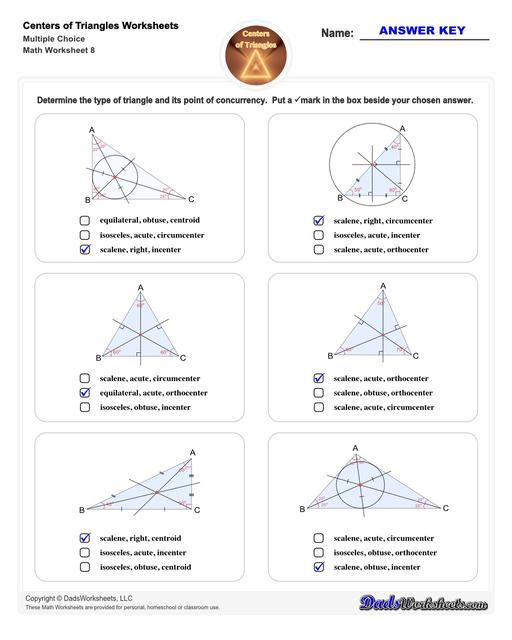
The second set of worksheets require students to identify the point of concurrency through multiple choice questions. The type of triangle by side and by angle will also be covered on this set.

And finally… worksheets that focus on finding the coordinates of centroid, orthocenter, circumcenter, and incenter are also available. All with answer keys!

Try some of the center of triangles worksheets below, or scroll down for more tips and ways on how to find the center of a triangle.

Centroid of a Triangle

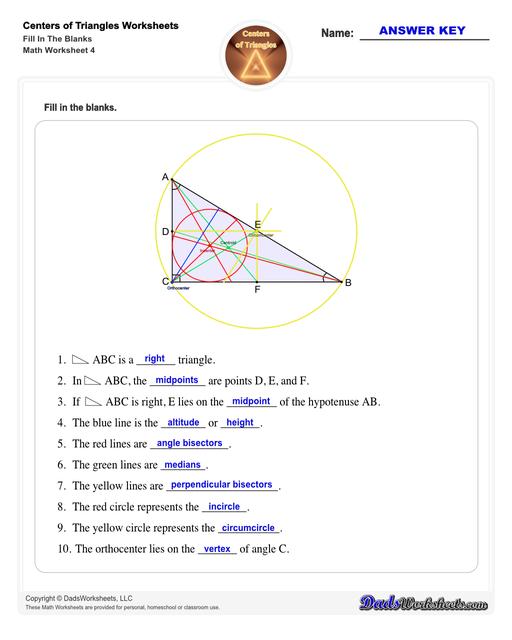
Refer to the figure above.

The lines from each vertex (corner) to the midpoint of the opposite side of the triangle are the medians. The point where all three lines intersect is the centroid.

Therefore, to find the centroid of a triangle, simply draw the medians (these are line segments that connect any vertex of a triangle to the opposite side). The point where all these three medians of the triangle meet is the centroid.

What are the properties of the centroid of a triangle?

It is always inside the triangle.

It always divides each median into segments in the ratio of 2:1, with the longer one near the vertex (as shown in the figure above).

It is the point of intersection or concurrency of the three medians of the triangle.

This diagrams illustrates the centroid of a triangle formula:

Where,

• x, y are the coordinates of the centroid of a triangle.
• x1, x2, x3 are the x coordinates of the vertices of a triangle.
• y1, y2, y3 are the y coordinates of the vertices of a triangle.

Orthocenter of a Triangle

Refer to the figure above.

The lines from each vertex (corner) of the triangle and is perpendicular to the opposite side are the triangle’s height or altitude.

The point where all three lines intersect is the orthocenter.

Therefore, to find the orthocenter of a triangle, simply draw the altitudes (these are perpendicular or straight lines that make an angle of 90°) from a triangle's side to the opposite vertex. The point where all these three altitudes of the triangle meet is the orthocenter.

What are the properties of the orthocenter of a triangle?

• It may lie outside the triangle.
• For any acute triangle, the orthocenter is always inside of the triangle.
• For any right triangle, the orthocenter is always at the vertex of the right angle.
• For every obtuse triangle, the orthocenter is always outside the triangle, opposite the longest leg.

Steps for Finding the Orthocenter of a Triangle

Step 1: Find the equation of one line.

Where,

• m is the slope of the line
• b is the y-intercept

Step 2: Find the slope of one side.

Where,

• m is the slope of the line
• x1, x2 are the x coordinates of the vertices of a triangle.
• y1, y2 are the y coordinates of the vertices of a triangle.

Step 3: Repeat Steps 1 and 2 to get the equation of another line.

Step 4: Calculate the slope that is perpendicular to the sides on previous steps

Where,

• m is the slope of the line

Step 5: Use the new slopes and the coordinates of the opposite vertices to find the equations of lines that form two altitudes.

Where,

• m is the perpendicular slope of the line solved in Step 4
• x, y are the coordinates of the vertex

Step 6: Use substitution to solve the system of two equations.

Circumcenter of a Triangle

This figure illustrates the circumcenter of a triangle:

The lines from each of the triangle’s midpoint to the opposite side are the triangle’s perpendicular bisectors. The circle that passes through all the vertices of the triangle is the circumcircle.

The center of the circumcircle and where all three lines intersect is the circumcenter.

To find the circumcenter of a triangle, simply draw the perpendicular bisectors (these are line segments which divide a triangle’s side into two equal parts at 90°) from each of triangle’s midpoints to the opposite side. It is not necessary that they should pass through the vertex of a triangle but passes through the midpoint of the sides. The point where all these three perpendicular bisectors of the triangle meet is the circumcenter.

What are the properties of the circumcenter of a triangle?

• It may lie outside the triangle.
• For any acute triangle, the circumcenter is always inside of the triangle.
• For every obtuse triangle, the circumcenter is always outside the triangle.
• For any right triangle, the circumcenter is always at the midpoint of the hypotenuse (the longest side).
• All three vertices of the triangle are equidistant from the circumcenter of a triangle.
• The circumcenter of a triangle is also the center of its circumcircle.

Steps for Finding the Circumcenter of a Triangle

You can use the formula shown in the diagram below to calculate the circumcenter of a triangle:

Where,

• x, y are the coordinates of the circumcenter of a triangle
• x1, x2, x3 are the x coordinates of the vertices of a triangle
• y1, y2, y3 are the y coordinates of the vertices of a triangle

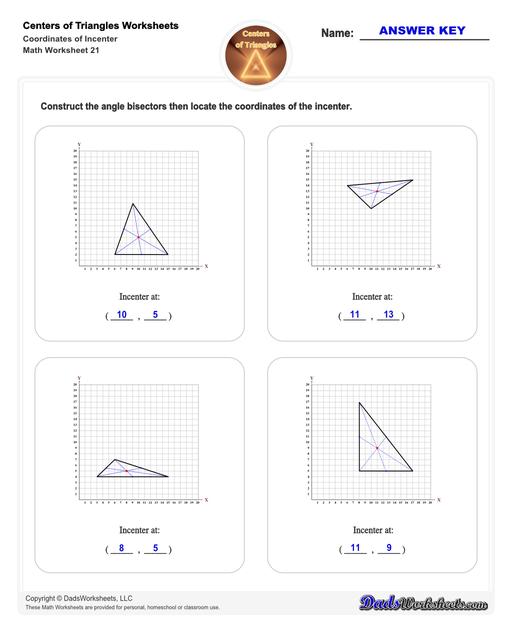
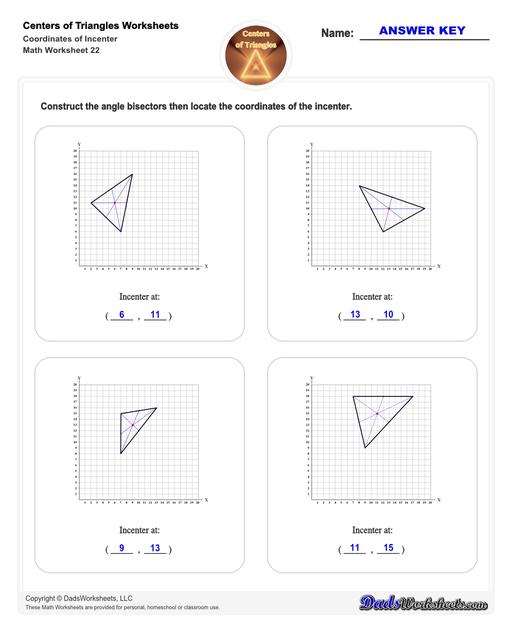
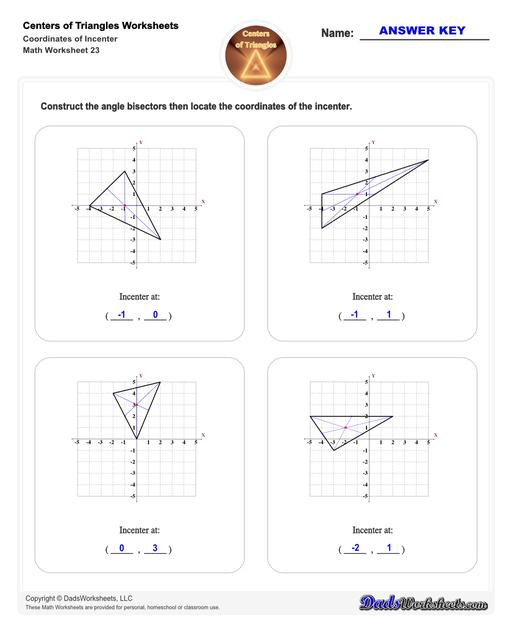
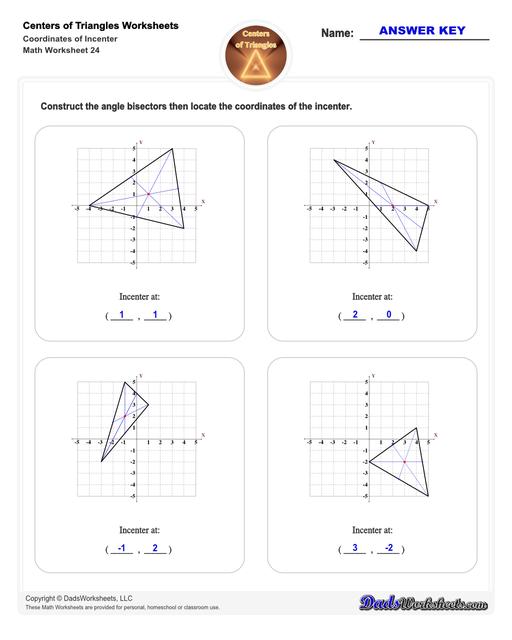
Incenter of a Triangle

This figure illustrates the incenter of a triangle:

The lines from each of the triangle’s vertex to the opposite side are the triangle’s angle bisectors. The biggest circle that can fit inside the triangle is the incircle. The center of the incircle and where all three lines intersect is the incenter.

To find the incenter of a triangle, simply draw the angle bisectors (these are line segments which divide an angle into two equal parts) from each of triangle’s vertices to the opposite side. The point where all these three angle bisectors of the triangle meet is the incenter.

What are the properties of the incenter of a triangle?

It is always inside the triangle.

It is always equidistant from the sides of the triangle.

The incenter of a triangle is also the center of its incircle.

How to Calculate the Incenter of a Triangle

You can use the formula below to calculate the incenter of a triangle formula:

Where,

• x and y are the coordinates of the incenter of a triangle.
• x1, x2, x3 are the x coordinates of the vertices of a triangle.
• y1, y2, y3 are the y coordinates of the vertices of a triangle.
• a, b and c are the lengths of the sides of a triangle.

More things to remember!

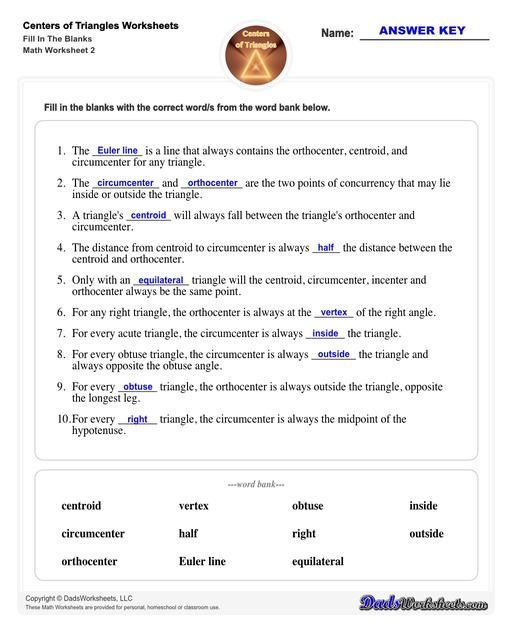
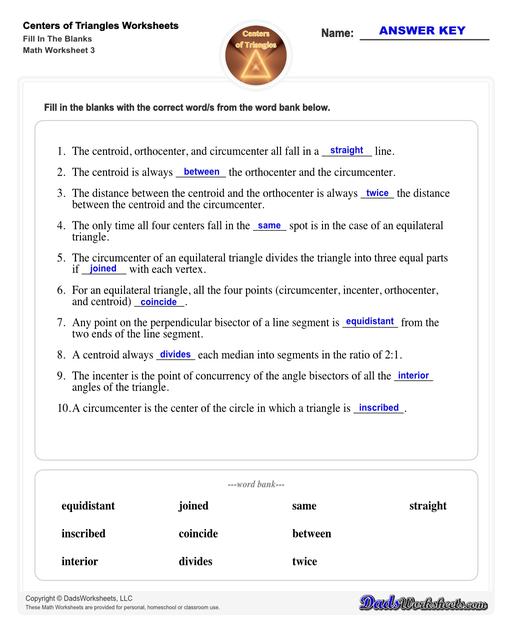
• The orthocenter, the centroid, and the circumcenter of a non-equilateral triangle are aligned. It means that they lie on the same straight line, called the “Euler line”.
• The only time all four centers (centroid, orthocenter, circumcenter, and incenter) fall in the same spot is in the case of an equilateral triangle.
• The centroid is always between the orthocenter and the circumcenter.
• The distance between the centroid and the orthocenter is always twice the distance between the centroid and the circumcenter.
• Both the circumcenter and the incenter have associated circles with specific geometric properties.
• Centroid is created using the medians of the triangle.
• Orthocenter is created using the heights(altitudes) of the triangle.
• Circumcenter is created using the perpendicular bisectors of the triangle.
• Incenter is created using the angles bisectors of the triangles.