Core Math Worksheets
Fraction Worksheets
Algebra
Other Worksheets
Place Value
Percentages
Rounding Numbers
Ordering Numbers
Standard, Expanded, Word Form
Mean Median Mode Range
Ratio Worksheets
Probability Worksheets
Roman Numerals
Factorization, GCD, LCM
Prime and Composite Numbers
Pre-Algebra
Geometry Worksheets
Blank Clocks
Telling Analog Time
Analog Elapsed Time
Greater Than and Less Than
Money
Arithmetic Sequences
Geometric Sequences
Venn Diagram
Graph Worksheets
Measurement & Conversions
Patterns and Puzzles
Color by Number
Holiday & Seasonal
Early Learning
Printables
Calculators
Math Worksheets by Grade
Worksheet News
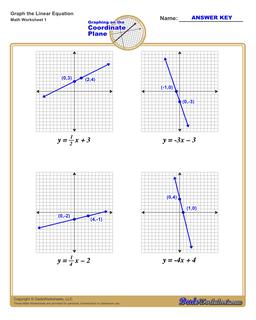
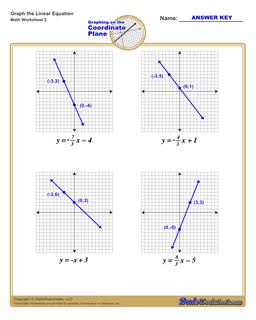
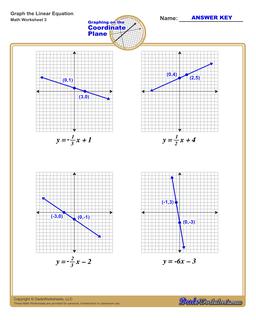
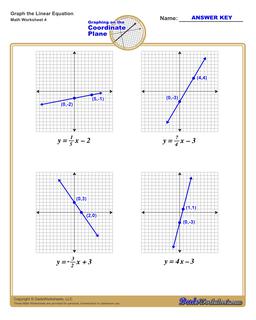
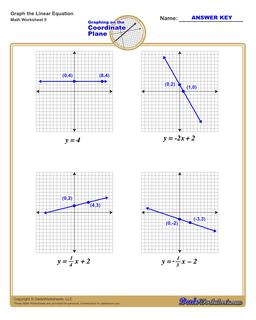
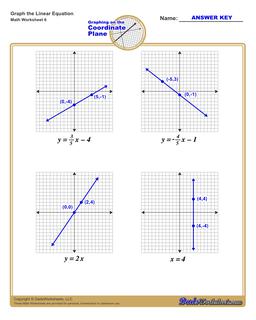
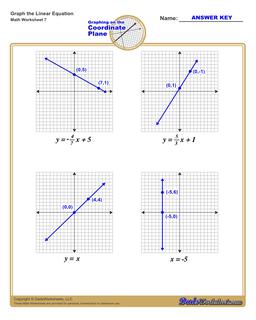
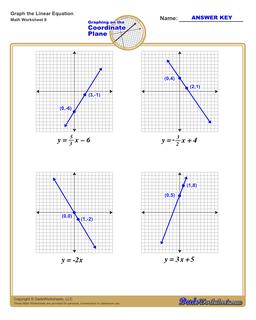
Graphing Linear Equations Practice
Each graphing linear equations worksheet on this page has four coordinate planes and equations in slope-intercept form, and includes an answer key showing the correct graph.
Graphing Linear Equations
What is Slope Intercept Form?
Equations that describe a line (i.e., a linear equations) are often expressed in a form called slope intercept form that looks like this...
Slope Intercept Form
An equation in slope intercept form shows how the y coordinate for a point on the line this calculated given an x coordinate. Slope in this equation is commonly labelled as 'm' and will take the form of a constant (an integer or a fraction) in the equation for an actual line. The y intercept value is 'b' value in the form, and will take the form of another constant that identifies where the line crosses the y axis (the point where the x value is zero). There are a few special cases where linear equations may not need all the parts of the slope-intercept equation and it's important to understand these forms so you know how to graph them.
Special Cases of Slope Intercept Equations
A slope intercept equation may not have its first term if the slope is zero. In those situation's the equation takes the form of horizontal line...
Equation for a Horizontal Line
A slope intercept equation may not have its second term (the y-intercept) if the line crosses the y-axis at the origin...
Slope Intercept Form Where Line Crosses Origin
For vertical lines, all of the points of the line are at the same x-axis value and the y coordinates are ignored. In those situation's the equation takes the form of vertical line...
Equation for a Vertical Line
How to Graph Linear Equations in Slope Intercept Form
If you have an equation in slope intercept form, you can use these steps to graph that equation on the coordinate plane:
Steps to Graph an Equation
- Identify the y-intercept constant in the equation (the 'b' term in the equation)
- Plot the y-intercept point on the coordinate plane at the (0,b) point.
- Identify the slope constant in the equation (the 'm' value in the equation). Convert it to a fraction over 1 or an improper fraction if it is not already in fraction form.
- Treating the slope as a rise-over-run value, start at the y-intercept move along the y-axis a distance equal to the value from the slope's numerator, and move along the x-axis a distance equal to the slope's denominator. Plot that point.
- Draw a line extending through the two plotted points.
You may also calculate the equation for a line by changing the slope independently (either as a slope fraction or a slope decimal), or by entering a new y intercept. If a new slope is entered, the slope calculator will move one of the points so that the equation matches the new line. If a new y intercept is entered, the slope will remain the same but the calculator will move the two points to shift the line to match the new y intercept.
If you are graphing linear equations, the worksheets on this page provide great practice resources for middle school students. You can also use a blank coordinate plane to graph your own equations, or try working with the slope calculator to see how different points, slope and y-intercept values can be combined to make an equation in slope intercept form.
What is the Slope of a Line?
The slope of a line is a mathematical measurement of how steep a line drawn on a graph appears, and this value is usually shown as the variable m in an equation in slope intercept form, y=mx+b.
Slope is defined as the ratio of vertical (y-axis) change over a given amount of horizontal (x-axis) change, often remembered more simply as a fraction describing rise over run or the rate of change. Slope is usually shown as an fraction, often an improper fraction, but it can also be represented as a mixed fraction or decimal number in some situations.
If a line is sloping up and to the right, it is rising as you look left-to-right across the x-axis. The rise in this case is positive, and such a line will have a positive slope.
If a line is sloping down and to the right, it is falling as you look left-to-right across the x-axis. The rise in this case is negative (the line is "falling"), and such a line will have a negative slope.
How to Find the Slope of a Line
If you have two points, they define a line on a Cartesian coordinate plane, and you can use those points to calculate the slope of the line. You can do that using the formula below…
Slope Equation
By starting with two points (x1,y1) and (x2,y2), the slope calculator substitutes the values into this equation to calculate the "rise" on the top and the "run" on the bottom. Given your two points. it doesn't matter which point is used (x1,y1) or (x2,y2), but it is very important that you consistently use the coordinates for each point. For example, if you choose one point such as (5, 6), be sure to use 5 as the first term of the subtraction on the top of the equation, and 6 as the first term of the subtraction on the bottom of the equation. Mixing the individual coordinates between points or thinking that there's some specific reason to choose one point as (x1,y1) are common mistakes calculating slope. When in doubt, check your answer with the slope calculator and you'll see it's a lot easier than it seems.
What is the Slope of a Horizontal Line?
The slope of a horizontal line is equal to zero. In the slope formula above, the top component of the slope ratio shows the vertical change between two points on the line. Because every point on a horizontal line will have the same y-axis coordinate, the numerator in this slope fraction will always be zero, and therefore the calculated slope will also always be zero.
The slope calculator will calculate the equation of the line without the first term, effectively reducing the y=mx+b equation to the form y=b, reflecting that the calculated y coordinate is constant for any given x coordinate.
What is the Slope of a Vertical Line?
Like the slope of a horizontal line, the slope of a vertical line is special. Again, referring to the slope equation, consider the way coordinates change as you travel up and down a vertical line. In the case of a vertical line, the x-axis coordinate will never change for any given y-axis coordinate. Because of this, the change in the x-axis represented as the bottom component of the slope ratio is zero.
There's a problem here. The slope equation divides by this change in x value result, and division by zero is not allowed. As a result, the slope of a vertical line is undefined, and you can readily see you cannot calculate y values in terms of x values using an equation in the y=mx+b slope intercept form because the m value for slope is undefined, making the whole equation undefined.
Simply put, there is not equivalent slope intercept form equation for a vertical line, so we need something else.
The equation for a vertical line is transformed by the slope calculator to the form x=c, where c represents a constant x value that defines the line for every possible y coordinate.
How to Find the Y Intercept of a Line
Once you have the equation of a line in slope intercept form, finding the y intercept is easy, but understanding why the equation highlights the intercept is as important as simply being able to read it from the equation's final term.
The y intercept is the point where the line crosses the y-axis. Because every point on the y-axis has an x coordinate value of zero, the line's slope intercept equation can be used to solve for y given an x value of zero. This will calculate the value where the line crosses the y-axis.
The y intercept is formally a coordinate pair, but because the x coordinate by definition zero, the y intercept is often only identified by a single value (the y coordinate).
Additionally, this y-axis value is alone as the b variable in the y=mx+b slope intercept equation. In fact, when a line is described as a slope intercept equation, the y intercept value can be read from the last term in the equation (the b variable).
However, the what if you don't have the line's equation and you're just starting from the points? The you can reshuffle the slope intercept equation so that it takes on the following form…
Intercept Equation
This formula calculates the intercept from the slope and one point on the line. The slope calculator uses this same formula to find the intercept after determining the actual slope as described above.
How to Find the Equation of a Line
Given the slope and at least one point, the b=y-mx equation is used to find the intercept.
With the intercept and slope calculated, all the parts necessary to create an equation in slope intercept form are present and can be substituted into the familiar y=mx+b form.