Core Math Worksheets
Fraction Worksheets
Algebra
Other Worksheets
Place Value
Percentages
Rounding Numbers
Ordering Numbers
Standard, Expanded, Word Form
Mean Median Mode Range
Ratio Worksheets
Probability Worksheets
Roman Numerals
Factorization, GCD, LCM
Prime and Composite Numbers
Pre-Algebra
Geometry Worksheets
Blank Clocks
Telling Analog Time
Analog Elapsed Time
Greater Than and Less Than
Money
Arithmetic Sequences
Geometric Sequences
Venn Diagram
Graph Worksheets
Measurement & Conversions
Patterns and Puzzles
Color by Number
Holiday & Seasonal
Early Learning
Printables
Calculators
Math Worksheets by Grade
Worksheet News
Pythagorean Theorem Worksheets
These Pythagorean Theorem worksheets require students to find the different sides of triangles using Pythagoras's theory establishing a relationship between the triangle's proportions.
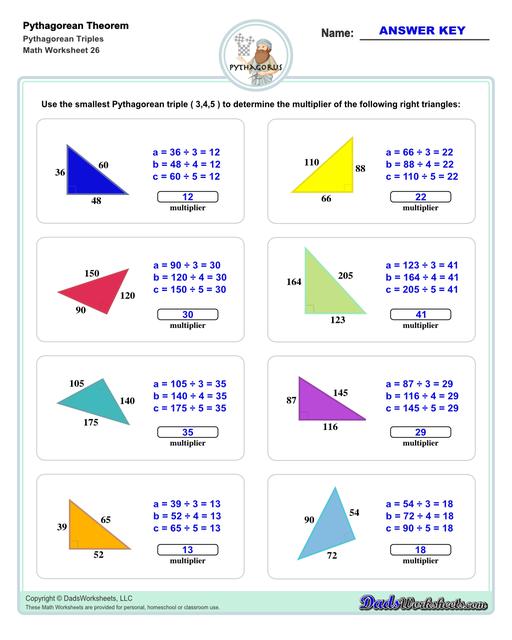
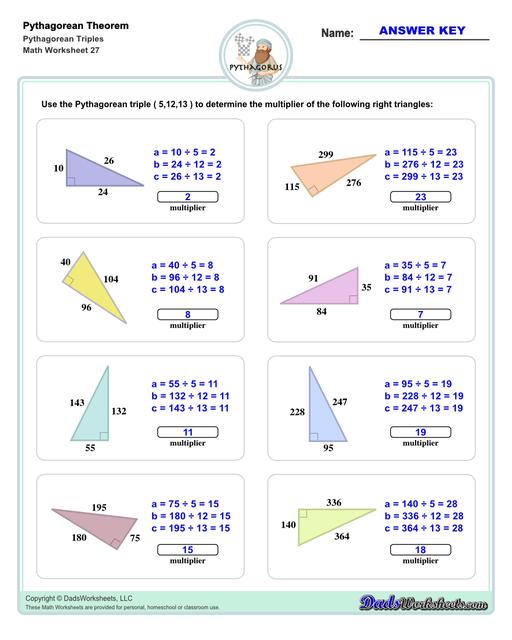
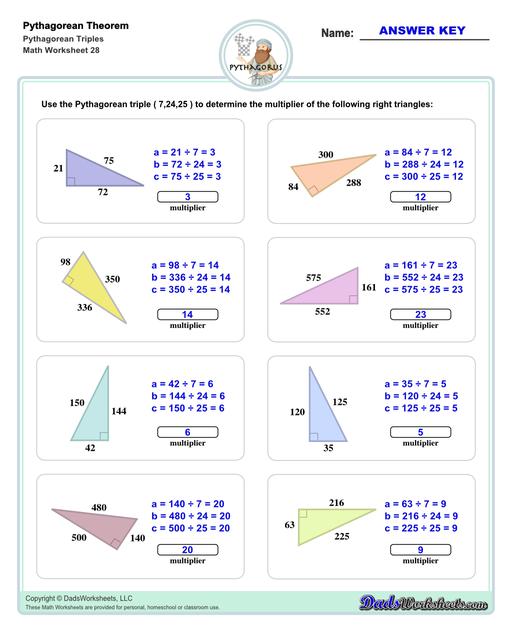
The first set of worksheets illustrates the Pythagorean Theorem visually, then common Pythagorean triples are given... These are definitely worth memorizing for standardized tests! This collection of worksheets finishes with more complex Pythagorean theorem problems for triangles, point-distance calculations and Pythagorean theorem word problems.
Try some of the pythagorean theorem worksheets below, or scroll down for tips and strategies for teaching the pythagorean theorem!
Pythagorean Theorem Charts
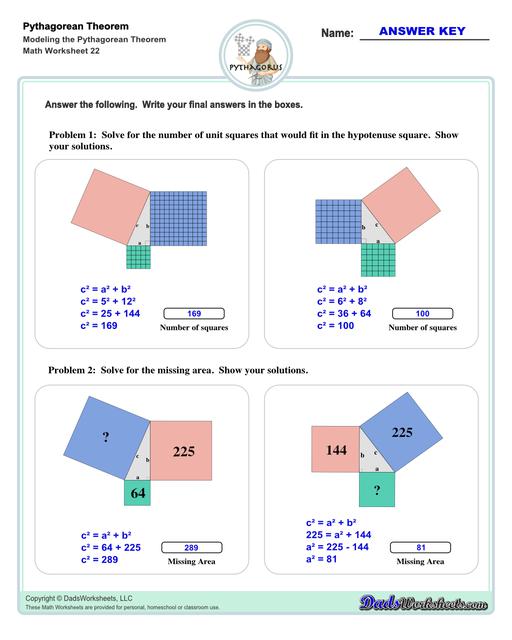
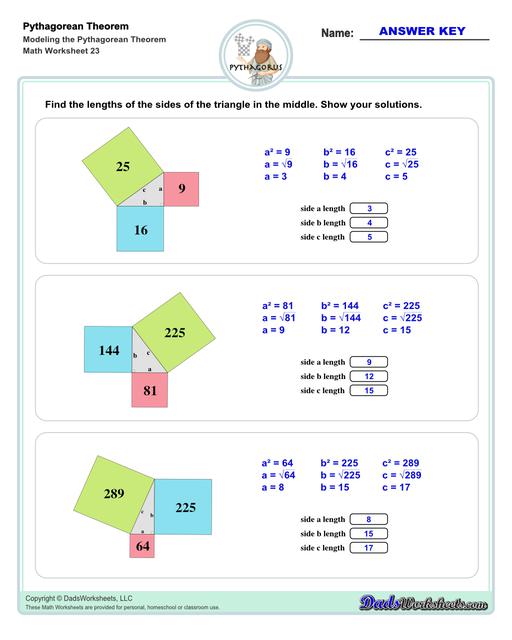
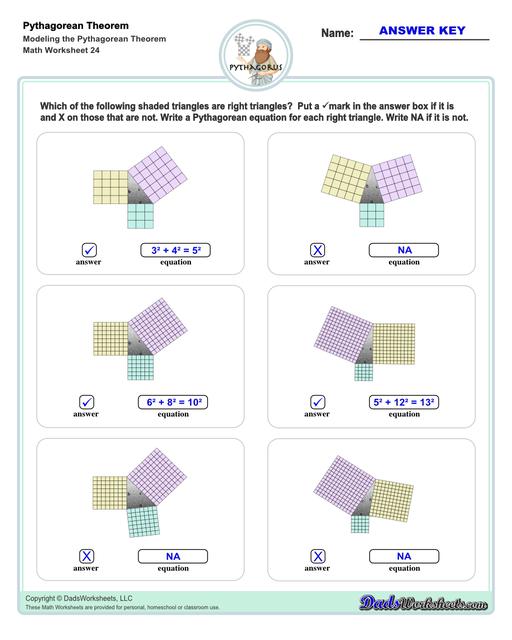
Visual Models of the Pythagorean Theorem
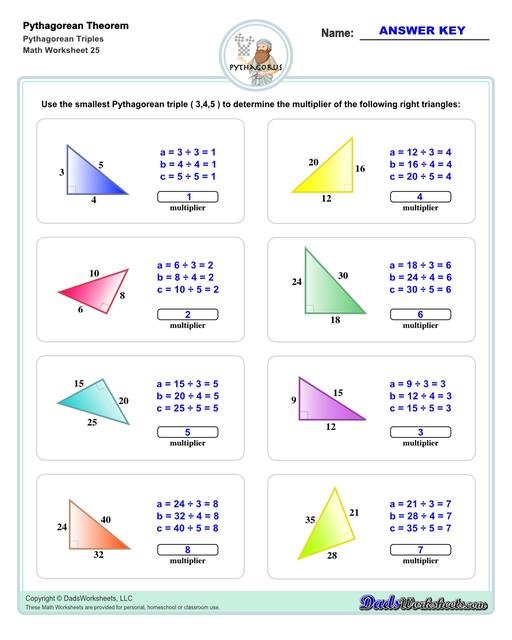
Pythagorean Triples Worksheets
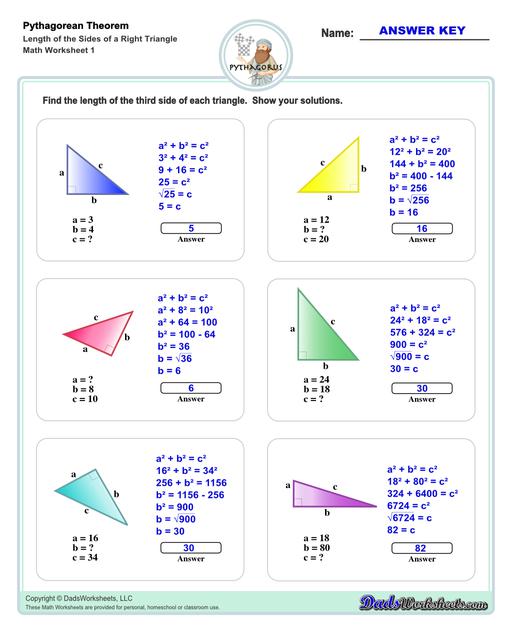
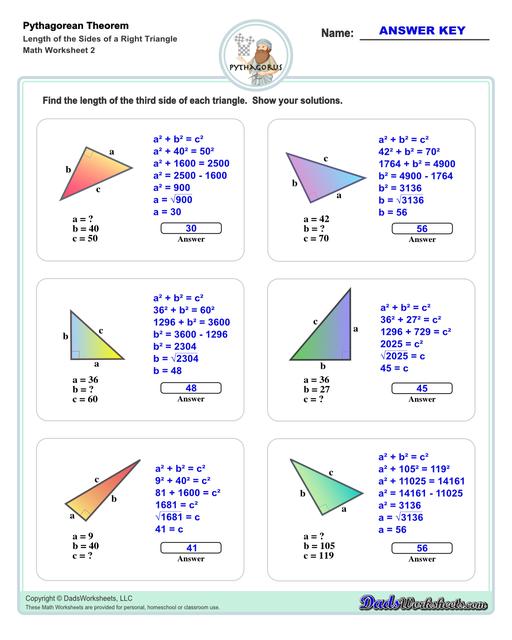
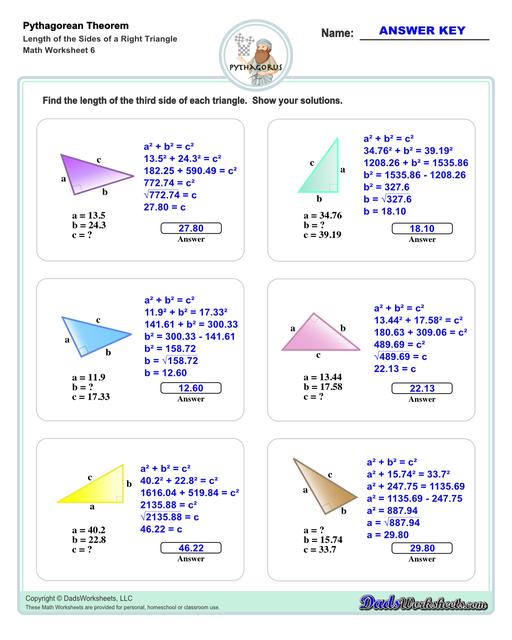
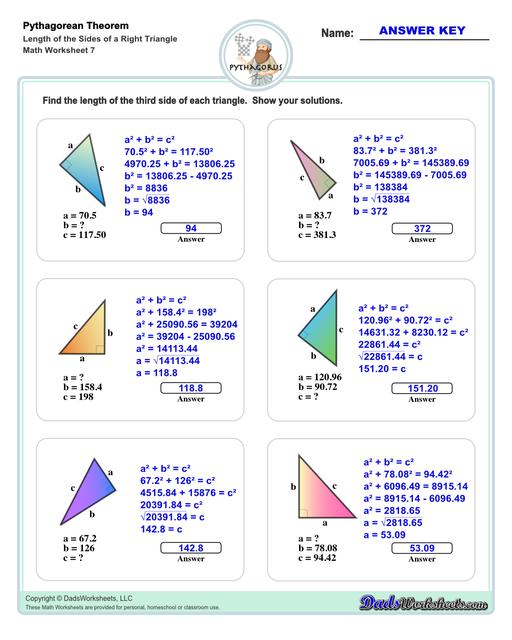
Sides of a Triangle Using the Pythagorean Theorem
Pythagorean Theorem Word Problems
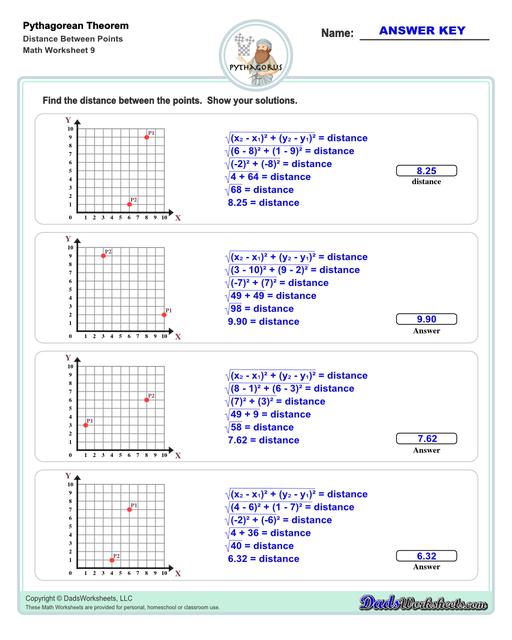
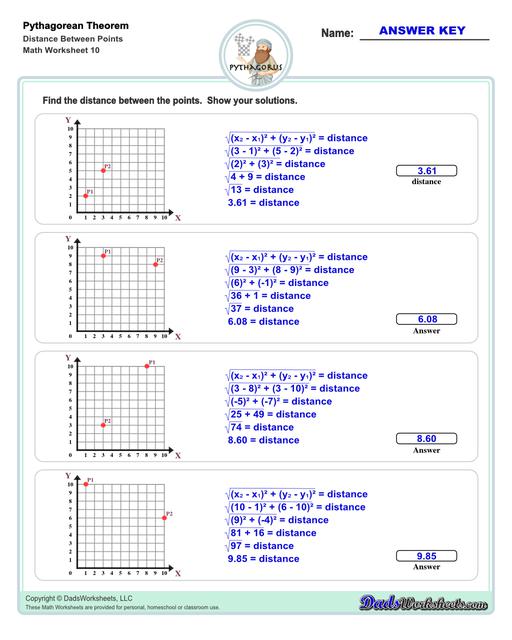
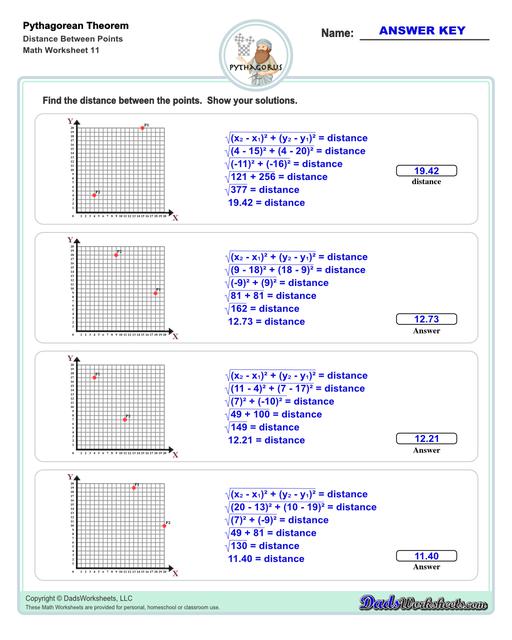
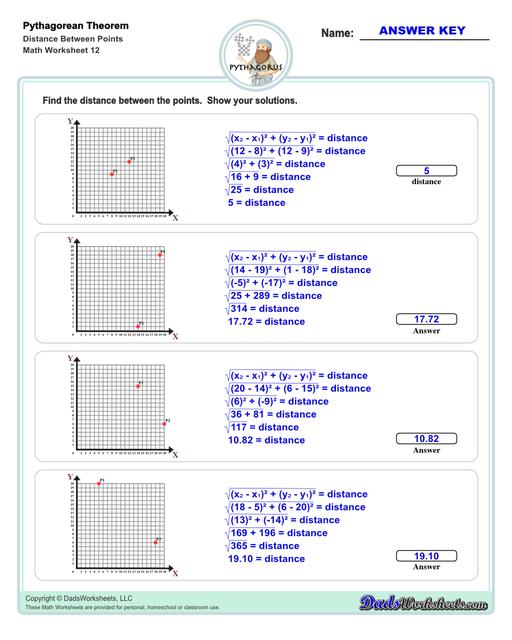
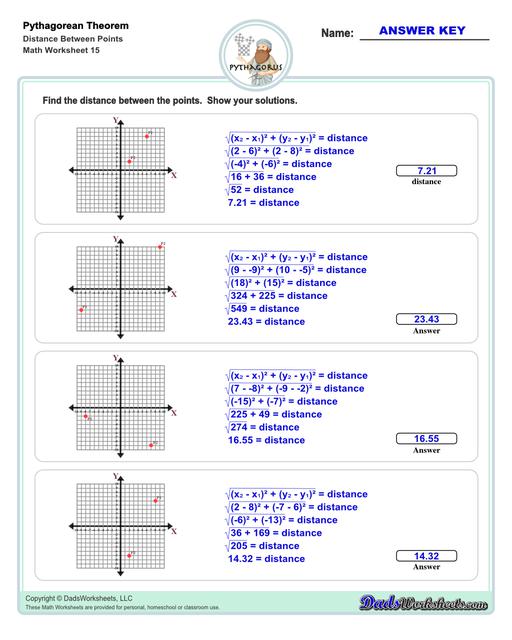
Distance Between Two Points Using the Pythagorean Theorem
What is the Pythagorean Theorem?
The Pythagorean theorem establishes the relationship between the sides of a right triangle. Using the Pythagorean theorem, you can find the hypotenuse (the long side) of a right triangle if you know the length of the other two sides. Or, if you know the length of the hypotenuse and the length of one of the sides, you can find the other side. Here's the actual equations:
Pythagorean Theorem
Another way to state this equation is to say that for any right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
If you are learning the Pythagorean theorem visually, you can see that this relationship isn't specific to square areas. It works for any shape whose area is proportionate to the dimension you assign to one of the triangles sides... This is worth understanding especially on some standardized tests where you may see the Pythagorean theorem proposed in a slightly different way. If you look at the Pythagorean theorem charts on this page, you can see these relationships correspond to other geometric shapes (like circles, or even regular polygons like a pentagon) derived from the lengths of the sides, but they all reduce to this same relationship.
Where Did the Pythagorean Theorem Come From?
While we commonly refer to this special relationship between the sides of a right triangle as the Pythagorean theorem and we assign its invention to the Greek philosopher Pythagoras of Samos (570BC-495BC), there is evidence that the Pythagorean theorem was understood by many other cultures significantly earlier. Ancient Babylonian tablets that date back to 1000 years before Pythagoras was born list out Pythagorean triples.
Even though Pythagoras may not have been the first person to come up with the theorem named after him, he was certainly one of the more prolific thinkers of his time in mathematics and other areas. He studied many areas of math and geometry, including regular solids and proportions. He believed the Earth was a sphere, in spite of many of his contemporaries thinking it's shape was planar. He was also an early proponent of vegetarianism.
Uses for the Pythagorean Theorem
The Pythagorean Theorem is one of the first geometry equations we learn and it has a variety of applications. Often these applications use the Pythagorean theorem to find the hypotenuse of a right triangle from two known lengths that make up the base and height of a right triangle. You don't have to be a rocket scientist to make use of the Pythagorean theorem; you'll find it's used reguarly in a variety of professions.
In construction you might find yourself using the Pythagorean theorem to figure out the area of a roof. If you know the tallest portion of the roof and the width of the building beneath it, you can find the actual length of the roof as the hypotenuse of the triangle, and then use that as part of a calculation to order shingles or other roofing material. Carpenters or concrete contractors will often use a 3-4-5 pythagorean triple to check if something is square when laying out wood working or a foundation.
In navigation and cartography, the Pythagorean theorem is used to find the distance between points on a map or the slope of a mountain or hill. The Pythagorean Theorem worksheets on this page have some similar problems for finding the distance (as the hypotenuse) between two points on a Cartesian coordinate plane.