DadsWorksheets.com - Thousands of printable math worksheets for teachers, home schooling or general study!
Share to PinterestPinterestShare to FacebookFacebookShare to PocketPocketShare to TwitterTwitterShare to EmailEmailShare to FlipboardFlipboard
Math Worksheets

Core Math Worksheets

Fraction Worksheets

Word Problems

Algebra

Other Worksheets

Measurement & Conversions

Patterns and Puzzles

Color by Number

Holiday & Seasonal

Early Learning

Printables

Calculators

Math Worksheets by Grade

Worksheet News

Shapes Worksheets

This is a collection of printable shapes worksheets and charts that cover the topics of the classification of basic shapes and two kinds of dimensional shapes, namely 2D and 3D shapes, and how to discern one from the other.

Check out our Shapes Chart, print them to familiarize your little ones with the basic shapes or try some of the printable shapes worksheets below. Test your skills! This is a great way for preschool and kindergarten students to learn the definitions of these shapes and practice differentiating them.

Shapes Charts

This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Chart 2d Basic ShapesShapes Chart 2d Basic Shapes
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Chart 2d Shapes Classification Of TrianglesShapes Chart 2d Shapes Classification Of Triangles
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Chart 3d Basic ShapesShapes Chart 3d Basic Shapes
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Chart List And Properties Of Geometric ShapesShapes Chart List And Properties Of Geometric Shapes

Shapes Crossword Puzzles

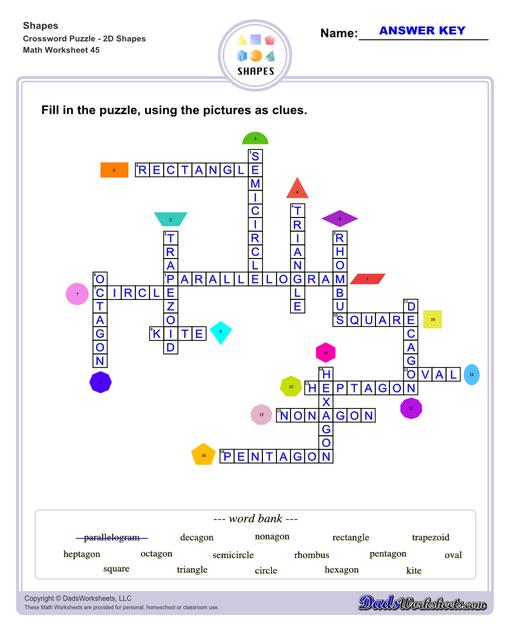
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Crossword Puzzle V1Shapes Crossword Puzzle V1
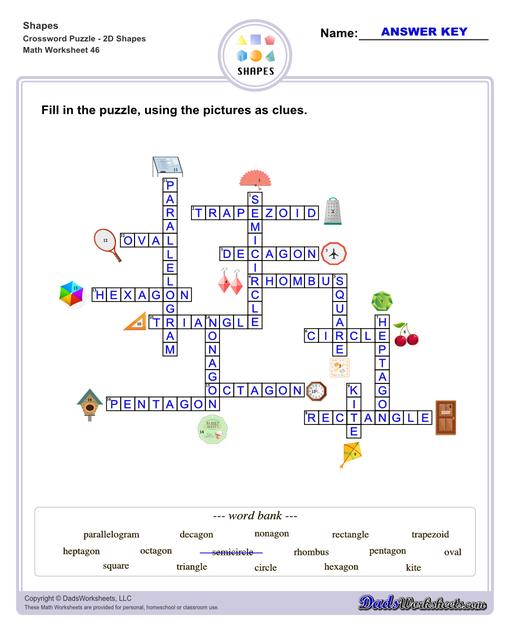
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Crossword Puzzle V2Shapes Crossword Puzzle V2
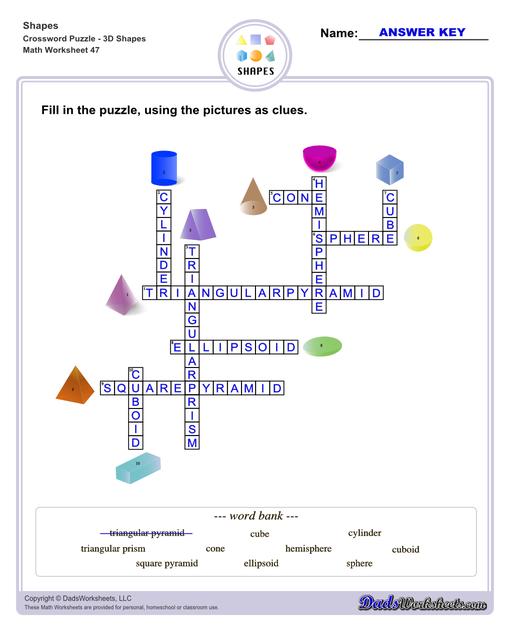
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Crossword Puzzle V3Shapes Crossword Puzzle V3
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Crossword Puzzle V4Shapes Crossword Puzzle V4

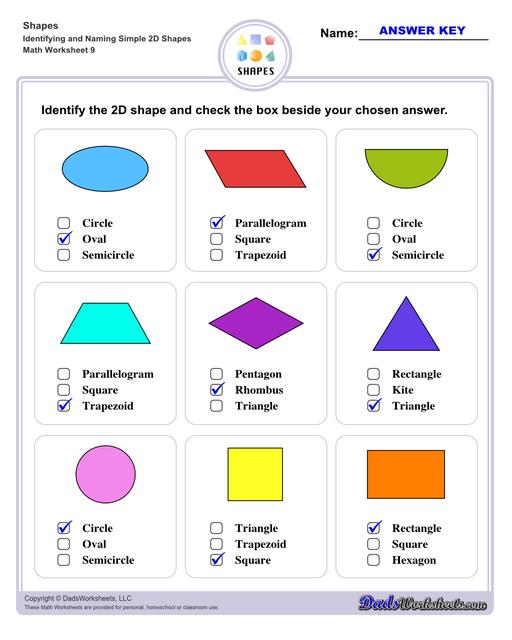
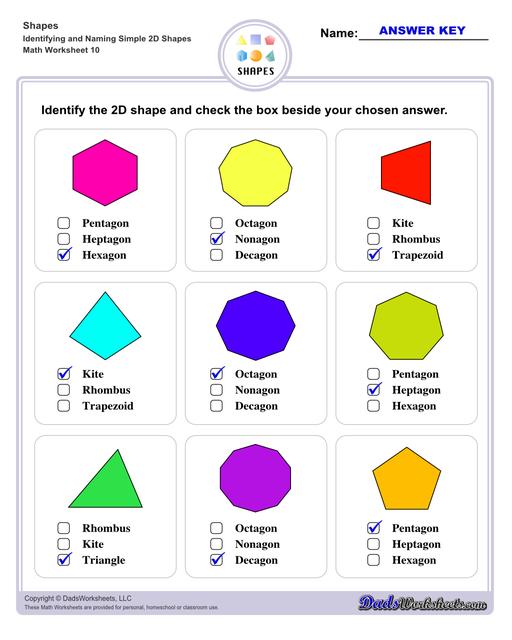
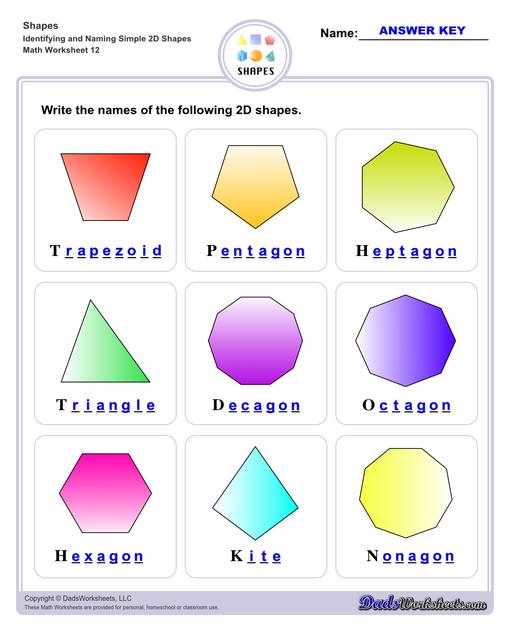
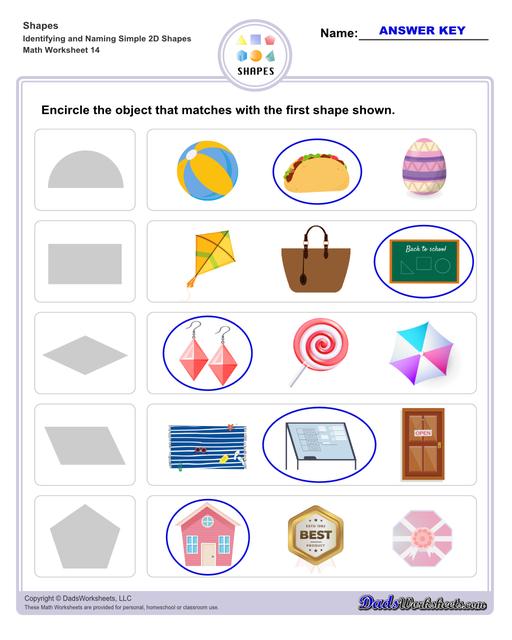
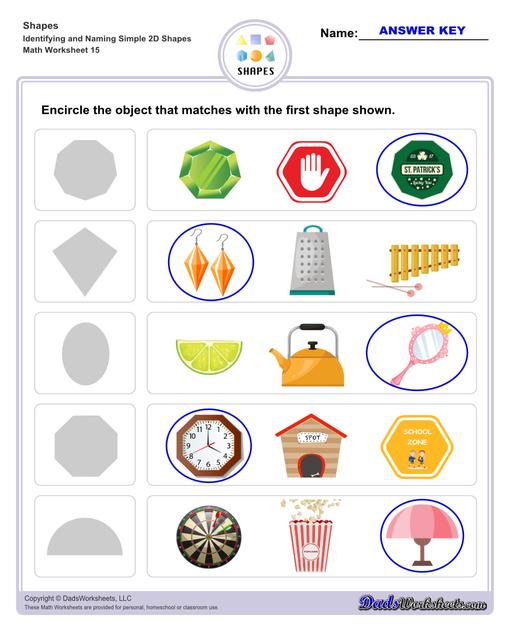
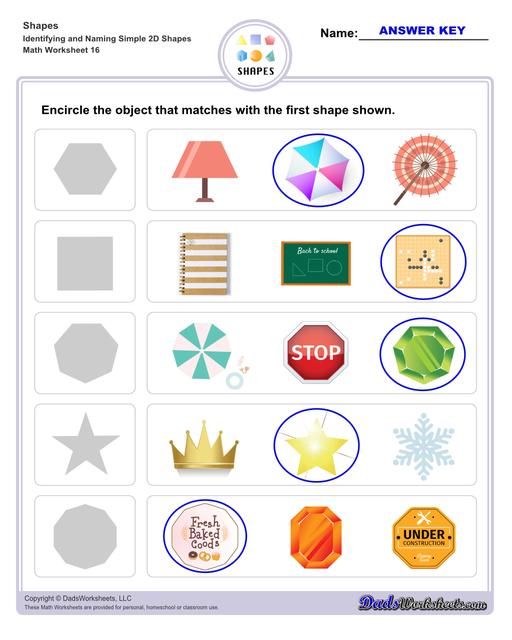
Identifying 2D Shapes Worksheets

This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Identifying And Naming Simple 2d Shapes V1Shapes Identifying And Naming Simple 2d Shapes V1
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Identifying And Naming Simple 2d Shapes V2Shapes Identifying And Naming Simple 2d Shapes V2
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Identifying And Naming Simple 2d Shapes V3Shapes Identifying And Naming Simple 2d Shapes V3
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Identifying And Naming Simple 2d Shapes V4Shapes Identifying And Naming Simple 2d Shapes V4
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Identifying And Naming Simple 2d Shapes V5Shapes Identifying And Naming Simple 2d Shapes V5
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Identifying And Naming Simple 2d Shapes V6Shapes Identifying And Naming Simple 2d Shapes V6
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Identifying And Naming Simple 2d Shapes V7Shapes Identifying And Naming Simple 2d Shapes V7
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Identifying And Naming Simple 2d Shapes V8Shapes Identifying And Naming Simple 2d Shapes V8

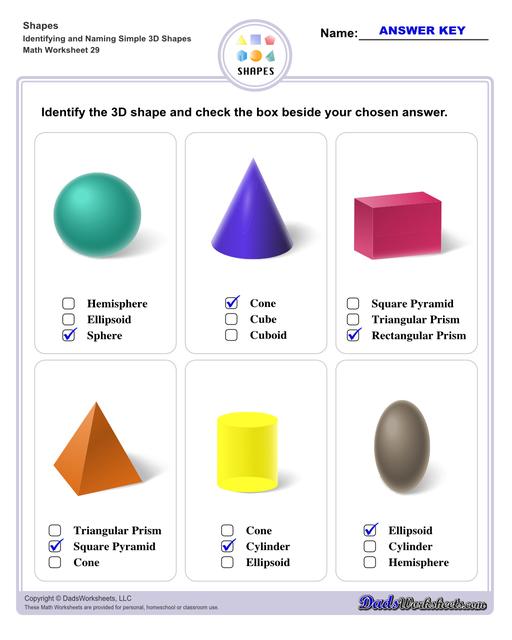
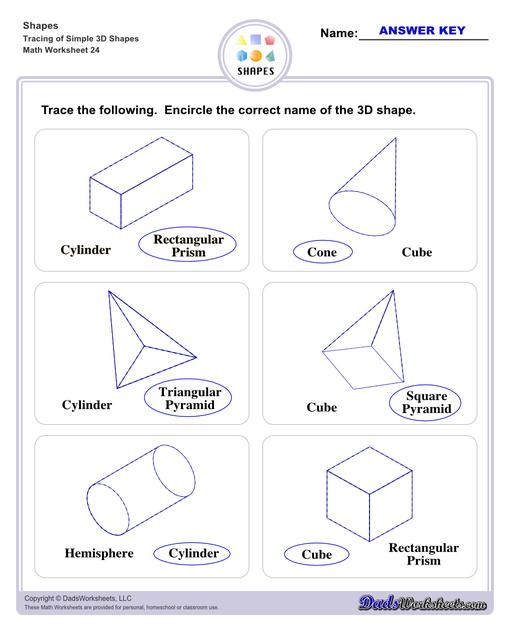
Identifying 3D Shapes Worksheets

This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Identifying And Naming Simple 3d Shapes V1Shapes Identifying And Naming Simple 3d Shapes V1
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Identifying And Naming Simple 3d Shapes V2Shapes Identifying And Naming Simple 3d Shapes V2
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Identifying And Naming Simple 3d Shapes V3Shapes Identifying And Naming Simple 3d Shapes V3
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Identifying And Naming Simple 3d Shapes V4Shapes Identifying And Naming Simple 3d Shapes V4
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Identifying And Naming Simple 3d Shapes V5Shapes Identifying And Naming Simple 3d Shapes V5
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Identifying And Naming Simple 3d Shapes V6Shapes Identifying And Naming Simple 3d Shapes V6
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Identifying And Naming Simple 3d Shapes V7Shapes Identifying And Naming Simple 3d Shapes V7
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Identifying And Naming Simple 3d Shapes V8Shapes Identifying And Naming Simple 3d Shapes V8

Tracing Shapes Worksheets

This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Tracing Basic 2d Shapes V1Shapes Tracing Basic 2d Shapes V1
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Tracing Basic 2d Shapes V2Shapes Tracing Basic 2d Shapes V2
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Tracing Basic 2d Shapes V3Shapes Tracing Basic 2d Shapes V3
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Tracing Basic 2d Shapes V4Shapes Tracing Basic 2d Shapes V4
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Tracing Basic 3d Shapes V1Shapes Tracing Basic 3d Shapes V1
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Tracing Basic 3d Shapes V2Shapes Tracing Basic 3d Shapes V2
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Tracing Basic 3d Shapes V3Shapes Tracing Basic 3d Shapes V3
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Tracing Basic 3d Shapes V4Shapes Tracing Basic 3d Shapes V4

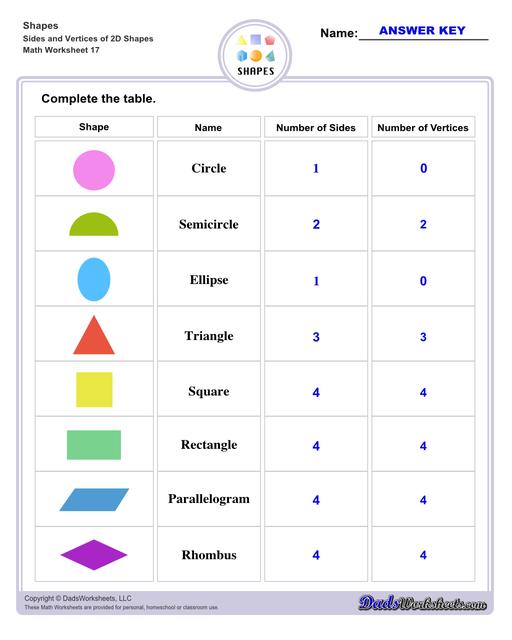
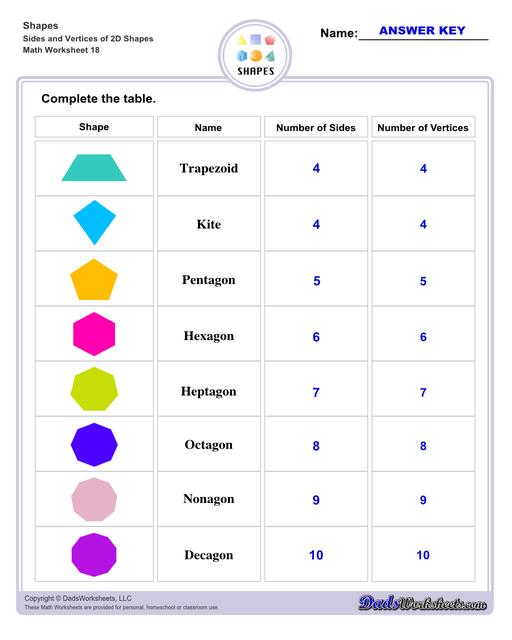
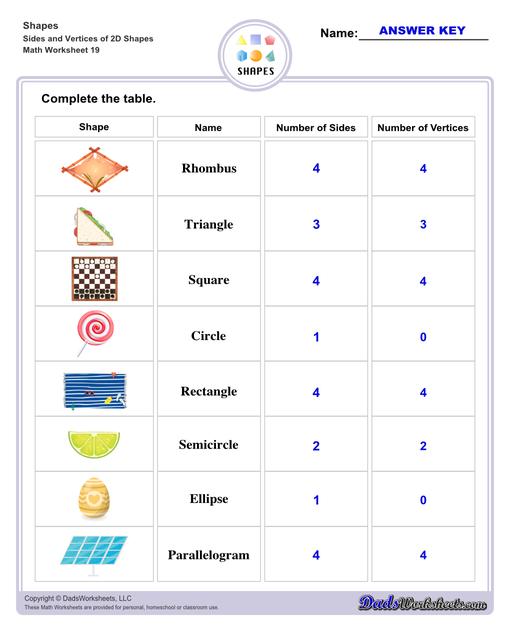
Sides and Vertices of 2D Shapes Worksheets

This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Sides And Vertices Of 2d Shapes V1Shapes Sides And Vertices Of 2d Shapes V1
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Sides And Vertices Of 2d Shapes V2Shapes Sides And Vertices Of 2d Shapes V2
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Sides And Vertices Of 2d Shapes V3Shapes Sides And Vertices Of 2d Shapes V3
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Sides And Vertices Of 2d Shapes V4Shapes Sides And Vertices Of 2d Shapes V4

Edges, Vertices and Faces of 3D Shapes Worksheets

This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Faces Edges And Vertices Of 3d Shapes V1Shapes Faces Edges And Vertices Of 3d Shapes V1
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Faces Edges And Vertices Of 3d Shapes V2Shapes Faces Edges And Vertices Of 3d Shapes V2
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Faces Edges And Vertices Of 3d Shapes V3Shapes Faces Edges And Vertices Of 3d Shapes V3
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Faces Edges And Vertices Of 3d Shapes V4Shapes Faces Edges And Vertices Of 3d Shapes V4

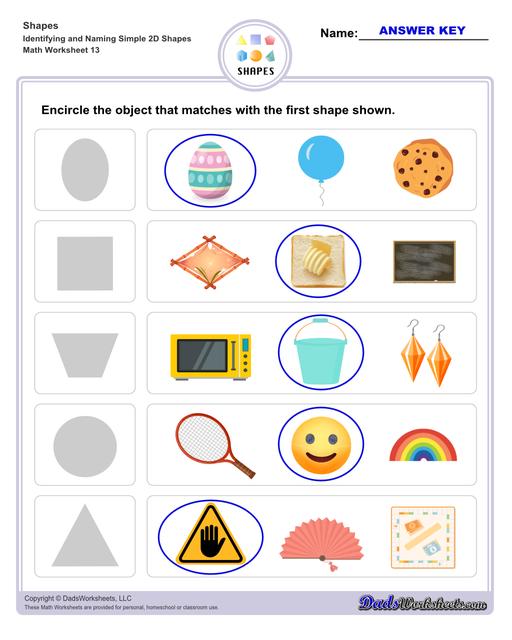
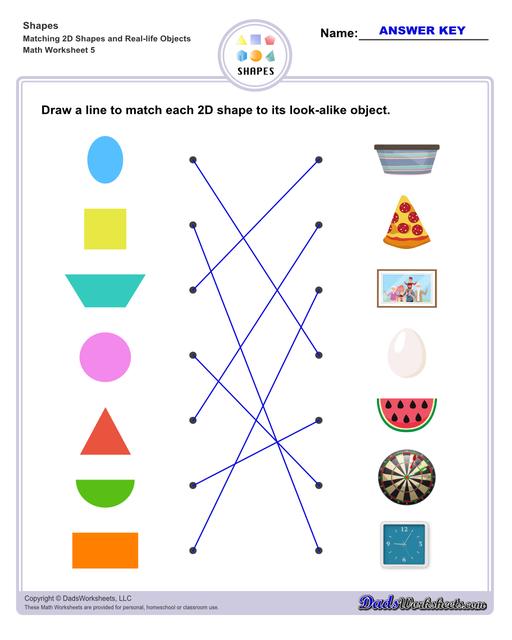
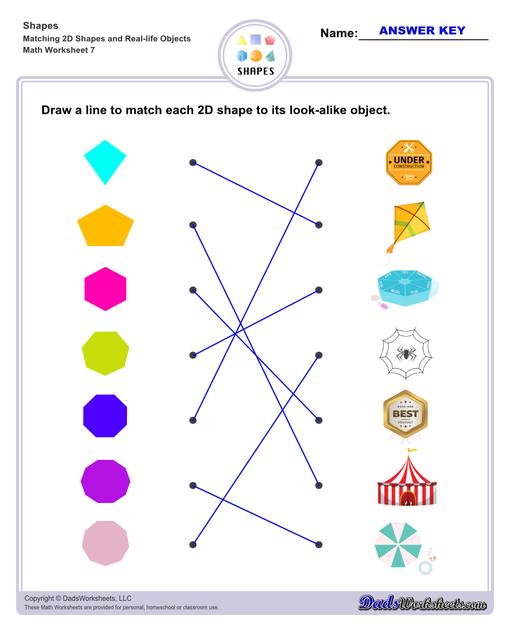
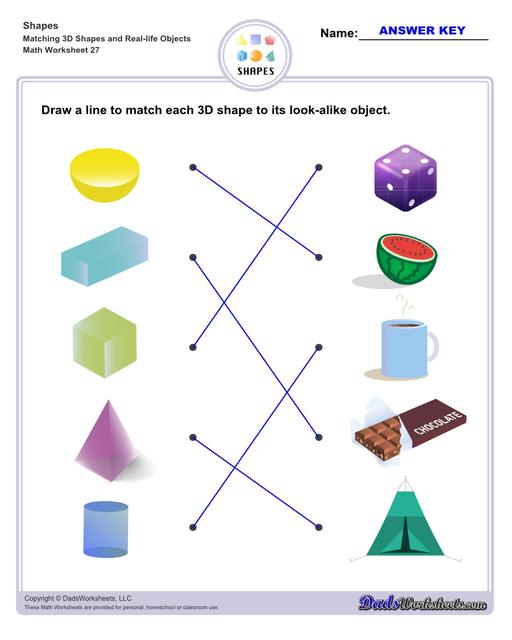
Matching Shapes Worksheets

This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Matching 2d Shapes And Real Life Objects V1Shapes Matching 2d Shapes And Real Life Objects V1
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Matching 2d Shapes And Real Life Objects V2Shapes Matching 2d Shapes And Real Life Objects V2
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Matching 2d Shapes And Real Life Objects V3Shapes Matching 2d Shapes And Real Life Objects V3
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Matching 2d Shapes And Real Life Objects V4Shapes Matching 2d Shapes And Real Life Objects V4
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Matching 3d Shapes And Real Life Objects V1Shapes Matching 3d Shapes And Real Life Objects V1
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Matching 3d Shapes And Real Life Objects V2Shapes Matching 3d Shapes And Real Life Objects V2
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Matching 3d Shapes And Real Life Objects V3Shapes Matching 3d Shapes And Real Life Objects V3
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Matching 3d Shapes And Real Life Objects V4Shapes Matching 3d Shapes And Real Life Objects V4

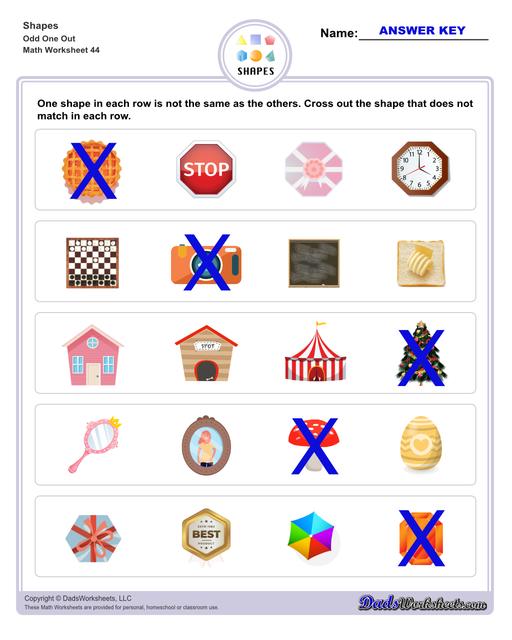
Which Shape Doesn't Belong Worksheets

This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Odd One Out V1Shapes Odd One Out V1
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Odd One Out V2Shapes Odd One Out V2
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Odd One Out V3Shapes Odd One Out V3
This page has dozens of printable shapes worksheets for identifying and naming 2D and 3D shapes. Activities for kindergarten and preschool age students include identifying counts of faces, edges and vertices. Students also learn to identify the shapes of real world objects, and practice worksheets include shape spelling and shape crossword puzzles. Shapes Odd One Out V4Shapes Odd One Out V4

Shapes Worksheets

The first few sets of worksheets on this page will help preschool and kindergarten students learn about shapes. The worksheets start out with tracing shapes, matching shapes, comparing them to real life objects, and naming and identifying the basic shapes.

The other set of worksheets are for first and second grade students. These worksheets cover the number of sides and vertices of basic 2D shapes, number of faces, edges, and vertices of 3D shapes. More worksheets like crossing out shapes that does not match with the group and even puzzle worksheets are also available to make learning shapes for kids more fun!All with answer keys!

What Are The Basic Shapes?

In preschool, children can learn to identify and name the basic 2d shapes. And as preschoolers learn to identify these shapes in their environment, they begin to develop an understanding of geometry. Now, what are these basic shapes that we first learn during our preschool days?

When we talk about the classification of shapes, there are 4 shapes that come into mind, the ones that we see in our everyday lives: rectangles, squares, circles, and triangles. But if we were to dig deeper and extend the list, more shapes to be included are the rhombuses, trapezoids, pentagons, hexagons, octagons, … the most commonly seen in nature and real life being circle (ball, cookie, round wall clock, etc.), but there are more shapes out there that we need to cover in order for you to get a grasp of what these really are. Now we’ve enumerated some of them, let us discuss the previously mentioned shapes in detail…

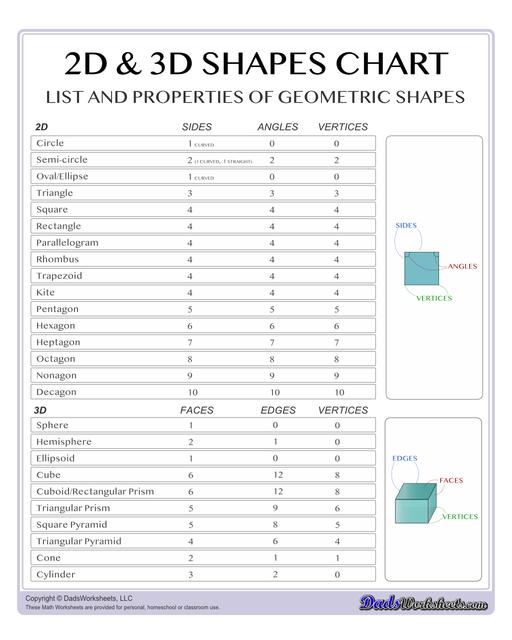
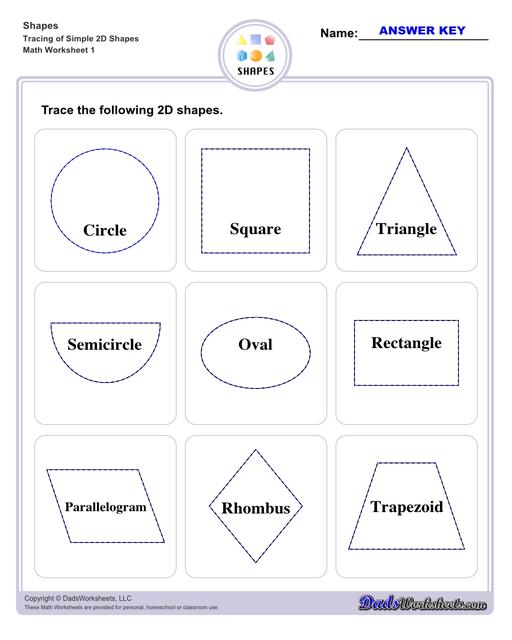
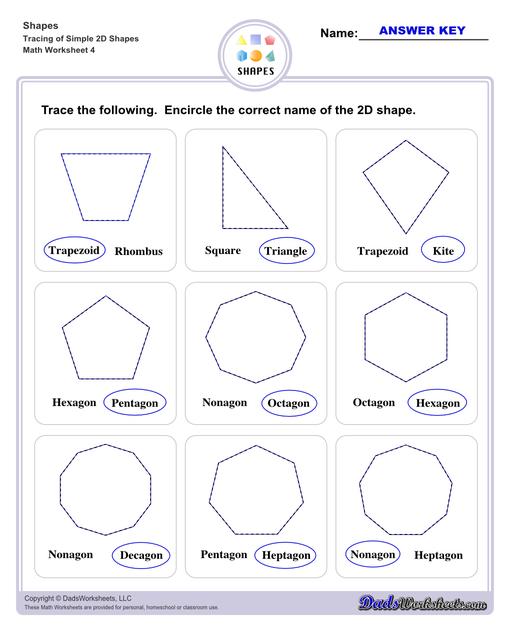
List of 2D Shapes

To start, let us first describe what 2d shapes look like:

Circle - a round shape that has a rotational symmetry around its center point, another key element of a circle is that it has no sides.

Semi-circle - divide a circle in half, cut it in equal parts along its diameter, and you basically have yourself a semi-circle.

Oval - also known as ellipse, a common figure for footballs, lemons, and specifically eggs. With that in mind, we can say that there are no lines to this shape and that it is elliptical in nature.

Triangle - contains exactly 3 sides and 3 angles. The sum of all three of its internal angles must be 180 degrees.

Square - with squares specifically, they must have 4 sides of the same length. Additionally, there must be 4 equal angles as well, each equal to 90 degrees.

Rectangles - have common attributes to the square such as having 4 sides and 4 right angles. This shape requires its parallel sides to be equal, thus making it so that its length to be longer whilst its width shorter.

Parallelogram - simply, it is a quadrilateral shape in which it has two pairs of parallel sides. The angles inside of the figure must have a sum of 360 degrees, and to demonstrate, squares, rhombi, and rectangles are all examples of parallelograms.

Rhombus - a type of parallelogram that has no right angles, rather it only uses opposite equal obtuse and acute angles. It uses the same measurements across the whole shape, like a square.

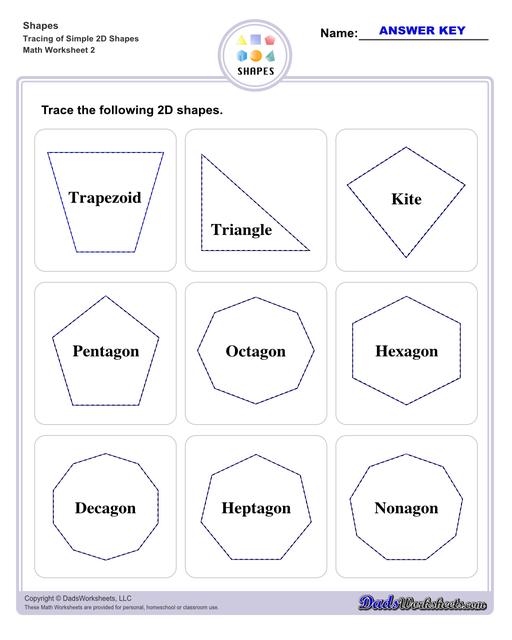
Trapezoid - yet again another type of parallelogram that only has one pair of parallel sides, while the other is non-parallel. Examples of trapezoids in everyday items could be the profile of lampshades, popcorn buckets, etc.

Kite - a shape associated with the diamond shaped toy that soars through the sky. But in a geometrical sense, it is a quadrilateral whose sides are grouped into 2 pairs of equal sides length-wise which are adjacent to one another.

Pentagon - a polygon that has 5 sides, and therefore has 5 angles.

Hexagon - a polygon that has 6 sides, and therefore has 6 angles.

Heptagon - a polygon that has 7 sides, and therefore has 7 angles.

Octagon - a polygon that has 8 sides, and therefore has 8 angles.

Nonagon - a polygon that has 9 sides, and therefore has 9 angles.

Decagon - a polygon that has 10 sides, and therefore has 10 angles.

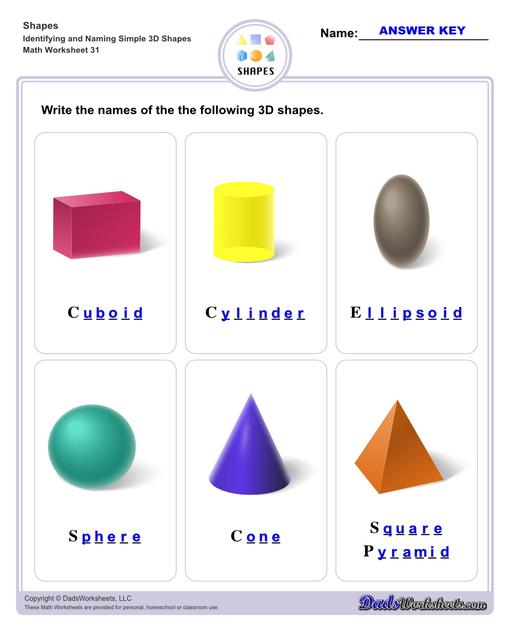
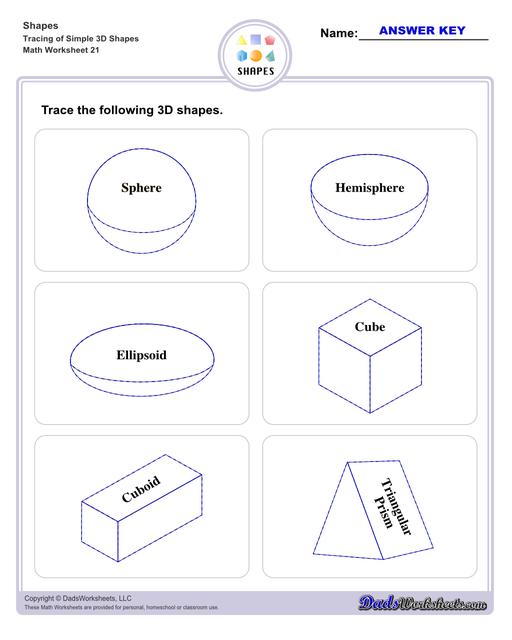
List of 3D Shapes4

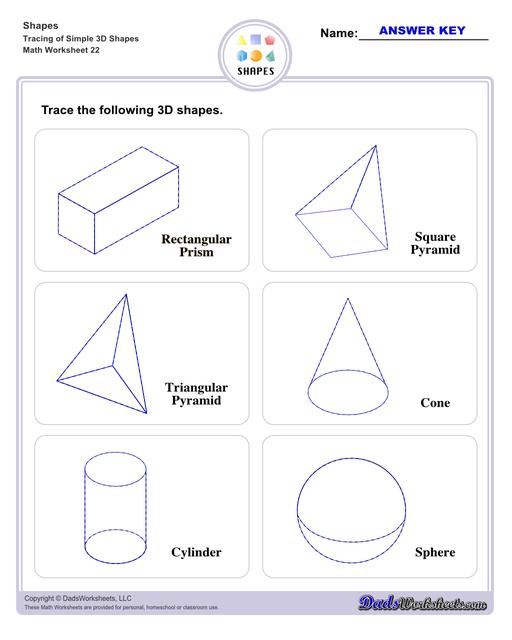
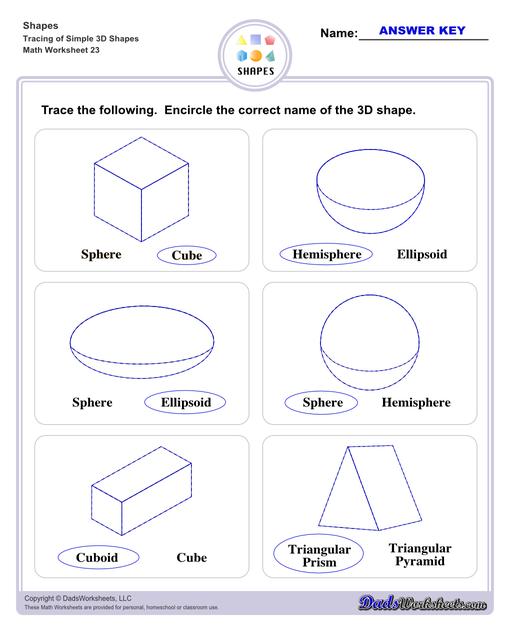
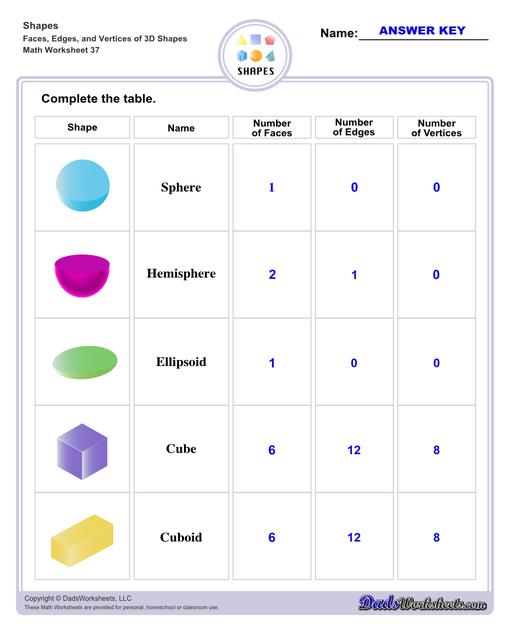
Sphere - it is round in profile and all its surface points have an equal distance from its center point.

Hemisphere - simply put, when you cut a sphere into two, you will get a hemisphere.

Ellipsoid - a stretched sphere that has an elliptical shape. Perfect examples of ellipsoids are eggs and footballs.

Cube - A 3 dimensional figure that has 6 congruent faces and 12 edges, the said faces being squares. Dice and Rubik's cubes are examples of cubes.

Rectangular Prism - also known as a cuboid, these shapes have bases that are congruent and parallel to each other; all of rectancgular prism's faces are rectangles. In simple terms, if all of its sides were tuned into squares, it would be a cube.

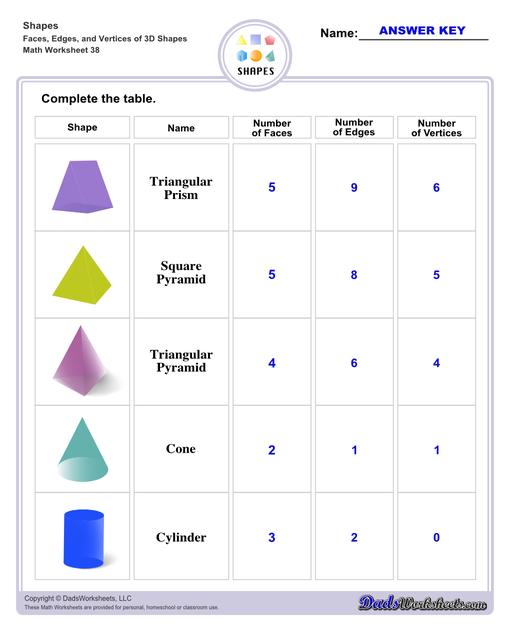
Triangular Prism - it is made up of two triangular bases and three rectangular sides.

Square Pyramid - it has a square base and 4 triangle faces pointed towards the top or its vertex.

Triangular Pyramid - it has a triangle base and 3 triangle faces pointed towards the top or its vertex.

Cone - a geometrical shape that starts from a flat circle base that narrows into a point called the vertex. A good representation of this shape may be an ice cream cone or a birthday hat.

Cylinder - somewhat similar with the cone in that it has a circle as a base, but for this shape, it has a flat circle for both top and bottom, which is then connected by a curved surface around the two bases, like a mug or a candle.

What Are Dimensional Shapes?

To give you a simple idea for what dimensional shapes may be, these examples just might help get your mind wrapped around the concept: a space is 3D and a plane is 2D. Simply put, they are figures in which they present the graphical representations of objects, and depending on each shapes’ characteristics, it can be determined to be a (x)D shape based on certain aspects we associate them with. (i.e. a shape that has width, height, depth, and is multidimensional = 3D figure) A more in depth discussion of the kinds of dimensional shapes will be presented in the following points as shown below.

Tips for Identifying 2D Shapes

As stated in prior points, a 2D shaped object will always have two dimensions. But if we get into the grit of it, this kind of shape is defined by its horizontal and vertical axes (x-axis and y-axis). They are characteristically flat … they also include length and width, unlike 3 dimensional objects that possess depth or height. And with this, we can definitively say that 2 dimensional shapes cannot be physically held as they are flat in nature; therefore, a clear description of this may be that a plane, when rotated to the side, it would become a line because again, it can be drawn on a flat surface as it only caters to the concept of having length and width. Examples consist of rectangles, triangles, hexagons, rhombuses… and anything that carries the listed attributes.

Tips for Identifying About 3D Shapes

When trying to figure out what a 3D shape is, we must ask ourselves the following questions: Does it have depth? Does it have height? Does it also have length and width? In reality, can it be physically held, unlike 2D shapes? Figures that fit these attributes are cubes, cuboids, cones, cylinders, and spheres. Unlike 2D shapes, when a 3 dimensional shape is turned to its side, multiple perspectives of this shape can be seen as it allows the visualization of depth and dimension. And with that, you can immediately spot the 3 dimensional shape from a group easily. If you are still confused, just remember the 4 descriptors that were explained prior.

Examples of 2D Shapes in Real Life

Circle - dart board, pie, cookie, coins, button, clock, hula hoop, car wheels

Semi-circle - slice of watermelon, rainbow, taco shell

Oval - oval mirror, badminton racket, oval face, leaves

Triangle - slice of pizza, half of a sandwich, sail boat

Square - chess board, monopoly board, table

Rectangles - picture frame, table, door rug, door, window

Parallelogram - architect’s desk, tiles, solar panels

Rhombus - sign board, traffic signs

Trapezoid - flower pot, hand bag, lamp, popcorn bucket, pail

Kite - flying kite, earrings

Pentagon - circus tent, dog house

Hexagon - road sign with 6 sides, umbrella with 6 sides

Heptagon - medicine box, candle holder with 7 sides

Octagon - medal, coins with 8 sides

Nonagon - fan, table, spider web with 9 sides

Decagon - dishes, coins, umbrella with 10 sides

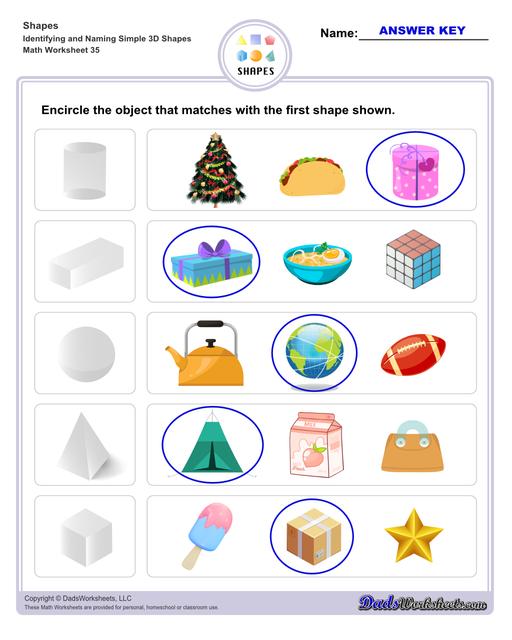
Examples of 3D Shapes in Real Life

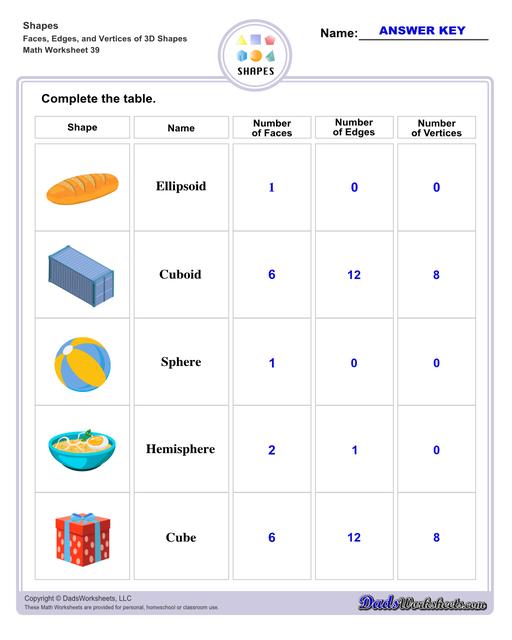
Sphere - basketball, volleyball, globe, balloon, lollipop

Hemisphere - half of a watermelon, soup bowl, dish cover

Ellipsoid - egg, football, lemon, bread

Cube - Rubik’s cube, cube box, gift box

Rectangular Prism - cereal box, chocolate bar, book

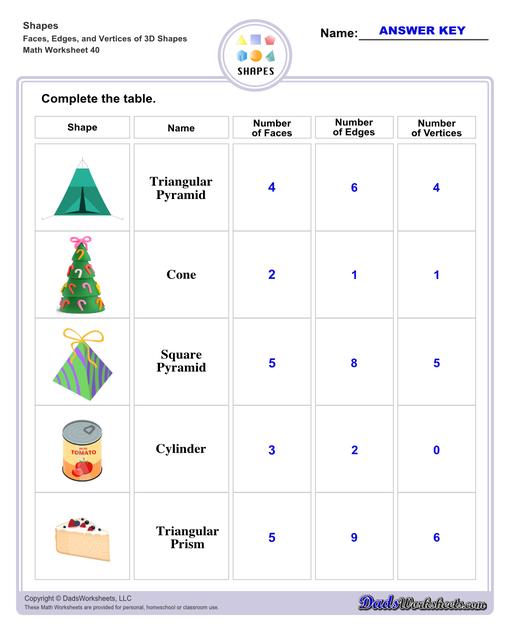
Triangular Prism - slice of cake, slice of cheese, camping tent

Square Pyramid - Pyramid of Egypt, camping tent, temples

Triangular Pyramid - camping tent, toys, tower

Cone - ice cream cone, party hat, christmas tree

Cylinder - mug, trash can, candle

Shapes Worksheets
WorksheetsCalculatorsAboutContactPrivacy