DadsWorksheets.com - Thousands of printable math worksheets for teachers, home schooling or general study!
Share to PinterestPinterestShare to FacebookFacebookShare to PocketPocketShare to TwitterTwitterShare to EmailEmailShare to FlipboardFlipboard
Math Worksheets

Core Math Worksheets

Fraction Worksheets

Word Problems

Algebra

Other Worksheets

Measurement & Conversions

Patterns and Puzzles

Color by Number

Holiday & Seasonal

Early Learning

Printables

Calculators

Math Worksheets by Grade

Worksheet News

Volume and Surface Area

The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area.

All of these worksheets include answer keys that break down the strategies used to solve the volume and surface area problems. In cases where multiple steps are required, each individual volume or surface area calculation is shown as well as how it is added or subtracted to get the final surface area and volume values for the answer.

Volume and Surface Area of Simple 3D Solids

The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Cubes And Rectangular Prisms V1 Cubes And Rectangular Prisms V1
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Cubes And Rectangular Prisms V2 Cubes And Rectangular Prisms V2
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Cubes And Rectangular Prisms V3 Cubes And Rectangular Prisms V3
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Cubes And Rectangular Prisms V4 Cubes And Rectangular Prisms V4
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Cylinders Cones And Spheres V1 Cylinders Cones And Spheres V1
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Cylinders Cones And Spheres V2 Cylinders Cones And Spheres V2
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Cylinders Cones And Spheres V3 Cylinders Cones And Spheres V3
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Cylinders Cones And Spheres V4 Cylinders Cones And Spheres V4
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Pyramids And Triangular Prisms V1 Pyramids And Triangular Prisms V1
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Pyramids And Triangular Prisms V2 Pyramids And Triangular Prisms V2
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Pyramids And Triangular Prisms V3 Pyramids And Triangular Prisms V3
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Pyramids And Triangular Prisms V4 Pyramids And Triangular Prisms V4

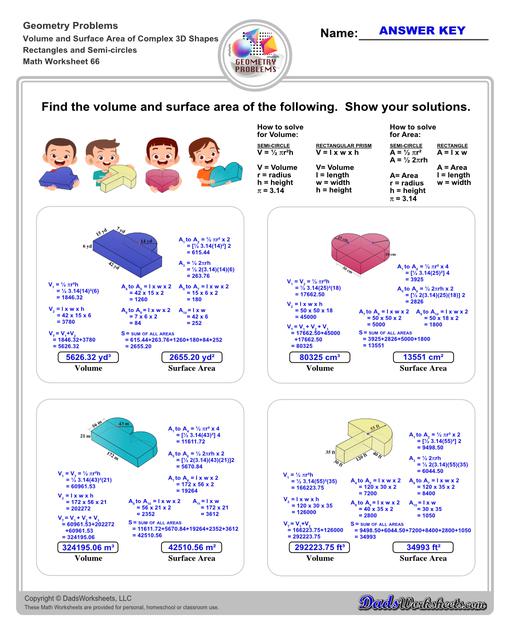
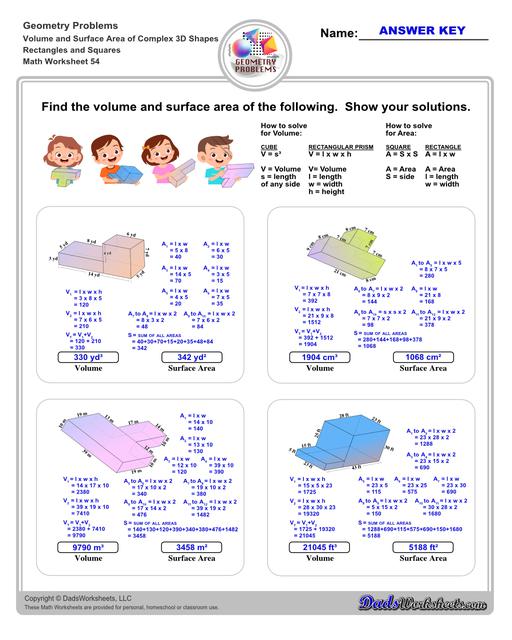
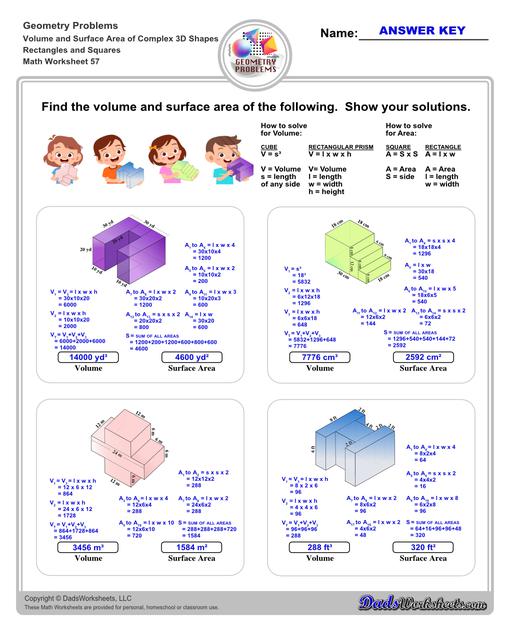
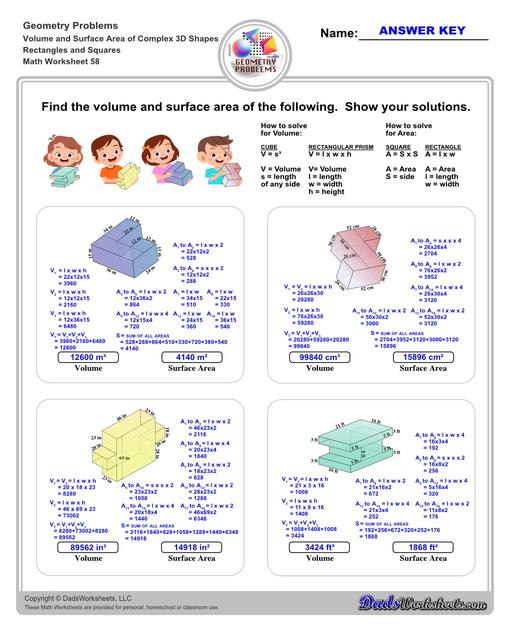
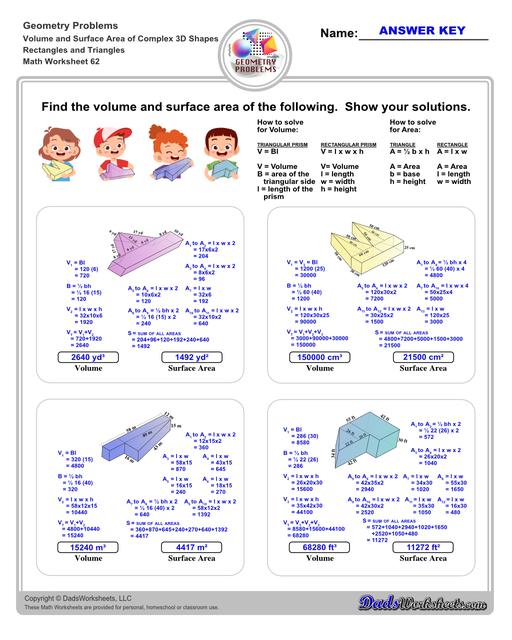
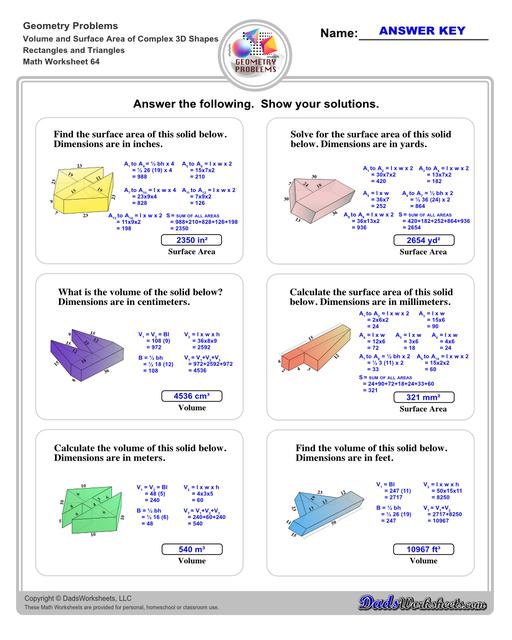
Volume and Surface Area of Complex 3D Solids

The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Rectangles And Semi Circles V1 Rectangles And Semi Circles V1
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Rectangles And Semi Circles V2 Rectangles And Semi Circles V2
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Rectangles And Semi Circles V3 Rectangles And Semi Circles V3
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Rectangles And Semi Circles V4 Rectangles And Semi Circles V4
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Rectangles And Squares V1 Rectangles And Squares V1
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Rectangles And Squares V2 Rectangles And Squares V2
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Rectangles And Squares V3 Rectangles And Squares V3
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Rectangles And Squares V4 Rectangles And Squares V4
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Rectangles And Squares V5 Rectangles And Squares V5
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Rectangles And Squares V6 Rectangles And Squares V6
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Rectangles And Squares V7 Rectangles And Squares V7
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Rectangles And Squares V8 Rectangles And Squares V8
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Rectangles And Triangles V1 Rectangles And Triangles V1
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Rectangles And Triangles V2 Rectangles And Triangles V2
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Rectangles And Triangles V3 Rectangles And Triangles V3
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Rectangles And Triangles V4 Rectangles And Triangles V4

Perimeter, Volume and Surface Area of Complex 3D Solids

The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Rectangles And Semi Circles V1 Rectangles And Semi Circles V1
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Rectangles And Semi Circles V2 Rectangles And Semi Circles V2
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Rectangles And Semi Circles V3 Rectangles And Semi Circles V3
The volume and surface area worksheets on this page start with requiring students to calculate area and perimeter of basic solids such as cubes, prisms, cones and spheres. Additional worksheets with compound shapes require students to calculate missing dimensions and use problem solving skills and strategies to calculate volume and surface area. Rectangles And Semi Circles V4 Rectangles And Semi Circles V4

Calculating Volume and Surface Area of Compound Solids

The worksheets on this page require students to calculate volume and surface area for solid shapes that composed from multiple extrusions or primitives. In some cases, the student is asked to calculate the perimeter of a 2D shape so that they can use the value to calculate the surface area of the extruded dimension. In other cases, the shapes are structured from subtracted solids, so the student will need to calculate a larger volume and then subtract the removed volume to arrive at the correct volume measurement.

Calculating the Surface Area of Simple Solids

Surface area of solids is calculated by adding up the surface area of the solid's individual surfaces. Here's a summary of the basic surface area formulas for primitive solids...

Shape Formula
Area of Cube A cube = 6 x 2
Area of Right Rectangular Prism A prism = 2lw + 2lh + 2wh
Area of Sphere A sphere = 4 π r 2
Area of Cylinder A Cylinder = 2πr2 + 2πrh
Area of Cone A Cone = πr r + h2+r2

Calculating Volume of Simple Solids

The volume of simple three dimensional solids van be calculated using the basic formulas you learned in 5th, 6th and 7th grade math classes. Here's a list of these volume formulas that you can use when completing the worksheets on this page...

Shape Formula
Volume of Cube V cube = x 3
Volume of Right Rectangular Prism V prism = lwh
Volume of Sphere V sphere =43πr3
Volume of Cylinder V Cylinder = πr2h
Volume of Cone V Cone = 13 πr2h
WorksheetsCalculatorsAboutContactPrivacy