Core Math Worksheets
Fraction Worksheets
Algebra
Other Worksheets
Place Value
Percentages
Rounding Numbers
Ordering Numbers
Standard, Expanded, Word Form
Mean Median Mode Range
Ratio Worksheets
Probability Worksheets
Roman Numerals
Factorization, GCD, LCM
Prime and Composite Numbers
Pre-Algebra
Geometry Worksheets
Blank Clocks
Telling Analog Time
Analog Elapsed Time
Greater Than and Less Than
Money
Arithmetic Sequences
Geometric Sequences
Venn Diagram
Graph Worksheets
Measurement & Conversions
Patterns and Puzzles
Color by Number
Holiday & Seasonal
Early Learning
Printables
Calculators
Math Worksheets by Grade
Worksheet News
Why Was the Student Afraid of the y-Intercept?
She thought she'd be stung by the b!
Bad math jokes aside, if you're a bit rusty on your graphing skills or just want to break out your y=mx+b, I have some worksheets you'll definitely appreciate!
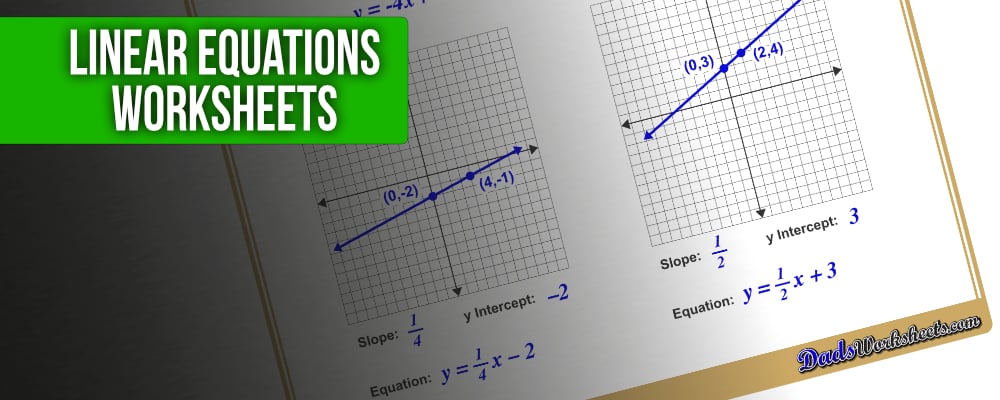
Linear equations come in many forms, starting from graphing lines in the familiar slope intercept form and progressing through solving systems of equations or even inequalities. As we’ve moved through various linear algebra topics, most of these variations have come up as areas that could benefit from some extra practice… and as you’d expect, I built out quite a number of printable linear equation worksheets to fill the bill!
A great place to start is this handy slope intercept form cheat sheet. It summarizes the key steps for graphing linear equations, or finding slope, intercepts and complete linear equation from two points. Print this out, stick it in your algebra binder, and then move on to the actual graphing worksheets!
A good place to start is learning how to graph equations in slope intercept form. A transition from this type of worksheet is to calculate slope from two points and identify whether slope is zero, positive, negative or undefined. The converse of graphing problems involves finding the equation of a line given two points, where kids will utilize those slope calculating skills. Another less commonly used form of linear equations is the point slope form, and of course you’ll find some practice worksheets for graphing these equations as well.
The section wraps up with more advanced linear equation worksheets including solving systems of linear equations by graphing and graphing linear inequalities. Another great tool to experiment while working with linear equations is this handy slope calculator. You can enter points, or enter a slope and an intercept, and it will give you the corresponding linear equation and a graph showing two points on the resulting line. It’s a great teaching tool, or just a quick way to knock that equation out if you have a couple of points laying around.
Graphing Linear Equations
More thoughts on linear equations? Let me know in the comments below!
